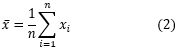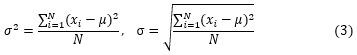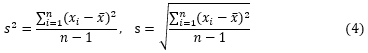はじめに

測量には誤差がつきものです。

というよりも測定・観測されたデータは必ず誤差を含んでいます。そして、測量の目的である成果（点の位置など）は、生データではなくデータを理論的に解析して求められるものです。従って、良い成果を得るためにはデータに含まれる誤差の性質と誤差のあるデータの解析法を知らなければなりません。

この連載では、データ解析の際に必要となる誤差論とデータ解析の基本的手法であるとともに最も良く使われている最小二乗法について平易に解説したいと思います。

誤差論や最小二乗法の基礎となるのが統計学です。

ガウスの時代から19世紀にかけて「記述統計学」が発展しましたが、20世紀に入ってそれに代わる「推測統計学」が生まれました。大量のデータを前提にした集団の性質を記述する記述統計学に対し、推測統計学は少ないサンプルから元の集団（母集団）の特性を推定し、それを検証する問題を扱うことができます。現在の衛星測位・測量成果の品質管理は、この推測統計学によって評価されています。

本講座は推測統計学に基づいていますが、お話の性質上、聞きなれない「母集団」のような用語や数式が出てくるのは避けられません。そのため高校程度の簡単な微分・積分、線形代数の知識は前提としますが、必要に応じて補足したいと思います。

1.誤差とは

1.1　観測・測定と誤差

私たちは、様々な目的のために観測・測定(注1)を行い、データを集めます。

しかし、データには同じ装置、同じ設定で測定等を繰り返したとしても、まったく同じ結果が得られることはないという不確実性が常に伴っています。不確実性の原因はさまざまな事柄が考えられます。

例えば、測定装置の問題、外部条件の変化、測定対象そのものの性質などですが、観測者・測定者の大きな目的の一つはそのような不確実性をなるべく小さくすることでしょう。

伝統的に、誤差とは

測定値－真の値（1）

と定義されます。

ただし、ここで注意していただきたいことは、私達は真の値(注2)を（理論値または定義された常数値の場合以外）厳密に知ることができないということです。知ることができるのは、真値の推定値にすぎません。

逆に言えば、真の値を知っていれば、その測定をする意味はないとも言えます。経験的には、同じ測定を何回も繰り返し平均をとれば、その値はある一定値に近づくと期待されます。

もし、その平均値（推定値）が「真値」に近づけばよい測定をしているといえるのですが、真値を知らないのでそれだけでは正しい推定値を導くことはできません。

• (注1)　観測と測定はここでは同義語として使っていますが、厳密にいえば、観測は対象を客観的に観察して記録し解析の基礎となるデータを得ること、測定は特に機器を用いて数値的データを得ることを指すようです。

 

• (注2)　ISOやJISでは、真とみなす値を参照値と定義し、真値の実在を扱っています。例えば、航空レーザー標高に対して、水準測量から得られた標高は参照値となり、真値とみなされます。私達の測量成果は「mm」単位で正確であればよいわけで、その範囲での正確な値は真値として扱うことができます。

1.2　測定値に含まれる誤差

一般に測定値には、以下に述べるランダム(偶然)誤差と系統誤差が含まれていると考えられます。

ランダム誤差

同じ測定を繰りかえした時に常に同じ結果を得るとは限りません。

結果は一致しないでばらつきますが、ばらつきの大きさや符号などが事前に確実にはわからない時、その測定にはランダム(偶然)誤差があるといいます。ランダム誤差は、確率論的に現れます。

確率論的という意味は、測定数を増やしていったとき、例えば、平均より大きい値と小さい値の数は等しくなる傾向にある、平均から大きく離れた値は少ない、などの性質を示すことです。

系統誤差

系統誤差は、(真値からの)偏りともいいますが、一定あるいは何らかの規則性(法則)によって確定できるものです。

系統誤差を除去するには、可能性のある原因を特定し、偏りの量を推定して測定値に補正を加えなくてはなりません。例えば、測定機器の較正が適切に行われていない場合や気象など外部条件の変化によって測定値にずれが生じます。

ただしランダム誤差と系統誤差は、上に述べたように概念的には違うものですが、実際には明確に分けることができない場合も多くあります。また、系統誤差であっても多くの測定を行ったときにランダム化が生じ、偶然誤差として扱う場合があります。例えば、光波測距儀による測定では日中や夜中では系統誤差となって現れますが、24時間観測でランダム化を行えば、偶然誤差として扱われます。

測定の誤差は上に述べたもののほかに、大きな誤差が観測者のミスや外部条件の一時的で急激な変化などで生ずる場合もあります。GNSS測位におけるマルチパスの影響も含まれます。この種の誤差(過失誤差)は、明らかにそれとわかることが多いので、注意深く観測を行うことで防ぐことができます。

1.3　精度と(正)確度

精度とは測定のばらつき(ランダム誤差)の尺度で、ランダム誤差が小さいほど精度が良いといいます。

一方、確度とは偏り（系統誤差）の尺度です。系統誤差が小さい時、確度が高いといいます。

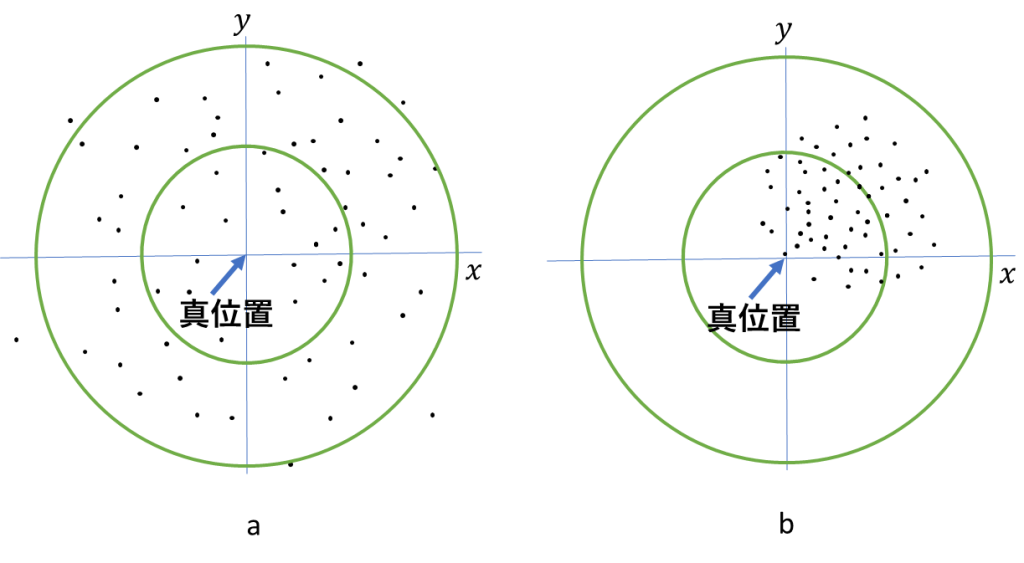
図1に精度と確度について水平位置の測位の例をあげました。ただし、広い意味ではばらつきと偏りを同時に考えて、どちらも小さい時、精度が良いということもあります。

また、新しい測定値評価のための概念として「不確かさ」というものもあります。これについては参考を見ていただきたいと思います。

図1．精度と確度（a. 低精度・高確度、b. 高精度・低確度） 

参考

測定誤差と不確かさ

測定結果の信頼性を表す指標として、近年では「不確かさ」という概念が登場しました。

不確かさは測定結果のばらつきの指標ですが、私達が測定しているのは真値ではなく真値に近いと思われる測定量であり、測定結果から得られるものはその推定値に過ぎないという考えが元になって定義されています。

測定誤差は真値という原理的に不可知な量から定義されるので、系統誤差も厳密には知りえず、誤差を使う測定結果の評価方法は明確には定義できないためです。

不確かさは、度量衡に関する測定機器の較正やトレーサビリティの確保、国際比較などに利用されるようになっています。

（不確かさについては、例えば、産業技術総合研究所による

https://unit.aist.go.jp/mcml/rg-mi/uncertainty/uncertainty.html

を参照してください。）

（第1回　誤差と統計 その2につづく）

2. 統計学の導入

統計学は、ばらつき（誤差）のあるデータから数学の手法でデータの性質や意味を見出す学問です。

私達も測定データを処理して目的とする情報(位置や高さなど)を適切に得るには統計学の助けを借りることになります。

2.1 母集団とサンプリング（標本抽出）

ある一つの量の測定を同一方法・条件で繰りかえし行うとその平均（系統誤差はないとして）は真の値に近づくと考えられます。

そこで、仮想的に無限回の繰り返しで得られる値の集まりを母集団(注3)と呼びます。母集団を知ることが観測の目的ですが、私たちは有限回の測定値しか手元にないため真の値は推定するしかありません。

統計学の言葉でいえば、母集団からの有限個のランダム（偏りのない）な標本値の抽出(サンプリング)によって、母集団のパラメータ(例えば平均値や分散など)の推定値を求めるということになります。統計学の用語では、母集団を特徴づけるパラメータを母数、その推定値を統計量といいます。

多数の測定をして得られた測定値は、すべてが同じではなく値には変動があります。そのため、平均だけではなく各測定値が平均からどのくらい変動しうるかも調べなければなりません。

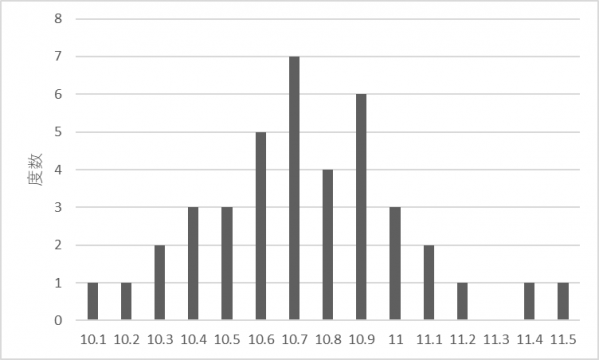
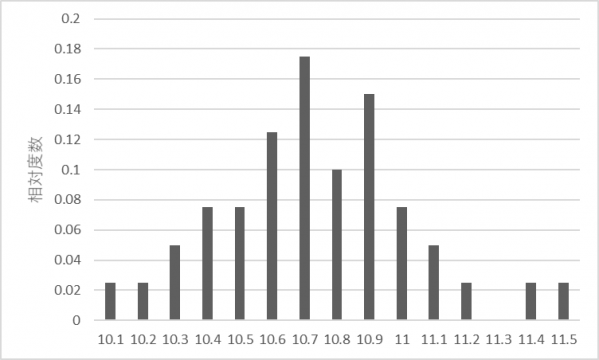
度数分布は測定値がどのように分布しているかを表したもので、変数(測定値)がある値をとる頻度を与えます(図2上)。度数を正規化して相対度数にすると、変数がある値をとる割合を示します(図2下)。

私たちが最終的に知りたいのはnを無限大にした分布ですが、これは後で述べる数学的に抽象化された確率分布につながっています。

図2．度数分布と相対度数分布（サンプル数：n=40）

• (注3)　母集団の要素の数を大きさと呼びますが、母集団の大きさは無限の場合と有限の場合があります。工業製品の抜き取り検査などでは有限ですが、ここで取り扱っているような同一条件での繰り返し測定や国民全体を対象とした調査などでは無限あるいはほとんど無限に近くなります。

2.2 基本的な概念

統計学で使われる基本的な概念について紹介しましょう。

平均(算術平均)

一つの量を繰り返しn回測定したとき、平均値は以下のとおりです。

中央値

n個の測定値を大きさの順に並べたときの中央の値のこと。

とすると、nが奇数なら中央値はですが、偶数の時はとします。

分散、標準偏差

平均値からのずれの2乗の平均が分散、その正値の平方根が標準偏差で測定値のばらつきを表します。

母集団の平均値が既知なら母集団の大きさをN（Nが無限ならNとする）として、

は、母集団分散と呼ばれます。

分散（標準偏差）には実はもう一つの式があります。

ここでnはサンプル数で、(3)式のNより当然小さくなります。

この式は、母集団のパラメータ推定という問題にかかわっています。母集団の値を推定するにはサンプリングを繰り返してその平均をとればよいと考えられます。

そのとき平均値の推定値は(1)と同じ式になりますが、標準偏差（分散）の推定値は(4)のようにnではなくn-1で割る式になります。ちなみに、式(4)のは、標本分散と呼ばれています。

参考文献

Meyer, S. L. : Data Analysis for Scientists and Engineers, John Wiley & Sons, 1992.

中川徹・小柳義夫: 最小二乗法による実験データ解析: 東京大学出版会, 1987.

東京大学教養学部統計学教室編: 自然科学の統計学, 東京大学出版会, 2016.

第2回は確率と確率分布についてです。

2018年11月から準天頂衛星の４機体制の運用が開始され、その活用によって、測量分野では、従来型の基準点測量が不要になるなど、その活用範囲が広がってきています。

当社技術顧問　松坂茂と中根勝見より、内閣府より示されているセンチメータ級測位補強サービス「CLAS」の精度の仕様の統計学的内容の解説及びCLAS利用にあたっての考慮すべき点などを解説します。

PDFダウンロードはこちらから

2019年07月19日から2019年07月31日を有効期間とする

地殻変動補正提供サービス パラメータを生成しましたので、お知らせいたします。

パラメータの精度評価結果は以下の通りです。

水平方向の推定誤差の平均値は、0.014 mです。

水平方向の推定誤差の標準偏差は、0.038 mです。

水平方向の推定誤差が4cm以下の地域の割合は、99.14％です。

なお、今回生成したパラメータは、すべての電子基準点のデータを使用し、

パラメータの生成および精度評価を行っています。

今後、パラメータと評価指標の精度向上のため、

解析条件を変更する可能性がありますので、予めご了承ください。