1.確率変数

前回お話したように、私たちが扱うデータは何らかの観測や測定をして得られたものです。

 

ただし、それらの値は厳密に求めることはできません。測定器の誤差や限界もあり、また、むやみに桁数を上げても意味のない場合がほとんどです。

 

測量でも普通、距離はmmまで測れば十分でしょう。体重でしたらg以下の値は様々な原因で変動するので意味がありません。

 

他方、私たちが知りたいものが平均的な値や傾向の場合もあります。例えば、物の値段や学力テストの結果などは、平均的な値が知りたいので、一つ一つの測定値は知りたい値の周りをばらつくこととなります。

 

従って、数値データにはつねに何らかの要因で変動、ばらつきが加わっています。

 

そのような偶然（ランダム）な変動を確率論の法則にしたがうとみなすことによって数学的な取り扱いを可能とし、得られたデータの分析や合理的な判断を下すための理論が統計学といえましょう。

 

ある変数の値が事前にわからずある確率で現れるとき、そのような変数のことを確率変数と呼びます。

 

確率変数には、サイコロの目のように離散的な値をとる場合もあれば、長さや重さのようにある範囲にわたって連続的な値をとることもあります。

 

2.確率とは

ここで、確率について基礎的なことをまとめておきます。少し数学的(抽象的)になりますが、現代の確率論は、幾何学や代数学と同じように公理（証明なしで成り立つものとする仮定）から出発して組み立てられます（注および参考文献1参照）。

 

確率の定義：

何かの実験を行うとして、起こりうるすべての結果の集合を標本空間S

標本空間の部分集合を事象Aとして

確率とは、各事象Aに対して数を与える関数で

確率の3公理

1. 

2. 

3. なら

を満たすもの。

 

（標本空間は標本という言葉を使っていますが、サンプリングの意味の標本とは異なりますので注意。または要素がない集合（空集合）です。）

 

集合を絵で表すとわかりやすくなります。

 

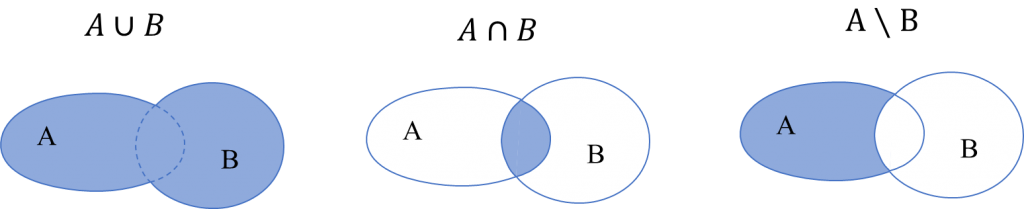
Sはすべての結果、事象は部分的な結果の集まりです(図1)。はAまたはBに含まれる結果、はAとBどちらにも含まれる結果、はAに含まれるがBには含まれない結果を示しています(図2)。

 

従って、はAまたはBの結果が起きる確率、はAとBが同時に起きる確率を示します。  は、得られた結果は必ずSの中にあるということを示します。

 

図1．標本空間とその部分集合の事象の例

 

図2．集合の和()、積（交わり）()、差()

 

ただし、事象を表す集合は「大きさ」が定義できるような集合であることが必要です。

 

確率は事象の「大きさ」を表すもので、それが定義できなければならないからです。事象はなんらかの結果を含んだものですが、他の結果との和や交わり、差もまた事象となります。

 

そのような操作を繰り返して作られた集合のあつまりとして事象が定義されています。

 

確率の公理から、いくつかの結果を導くことができます。

AとBを任意の事象として、

 

(1)は当然ですし、(2)は図2と公理3を使って証明できます。

 

条件付き確率と独立事象

ある事象Aの確率を考えるとき、他の事象Bが起きたか起きなかったかでその確率が影響されるときがあります。B が起こった時にAが起きる確率を条件付確率といい、つぎのように定義されます。

 

変形すると      

 

となります。

 

また、AとBがお互いに影響を及ぼさない場合、二つの事象は独立といい、ですから二つが同時に起きる確率は(4)より次のようになります。

 

 

確率変数の定義

1．で述べた確率変数を数学的に定義すると、確率変数とは標本空間Sの要素である結果に実数値を対応させる関数です(図3)。

 

例えば、コインを投げた時、表を1、裏を0とすれば結果は0と1で表せますし、サイコロでしたら、出た目の数を確率変数とすれば、結果は1から6の数字で表せます。

 

長さや重さの場合は、測定値をそのまま確率変数と考えることができます。

 

また、確率はもともと事象に対して定義されているので、確率変数の値の集合はもとの事象と対応づけられていることが必要です。

 

文献では、確率変数は大文字で、実現値は小文字で書かれることが多いようです。

 

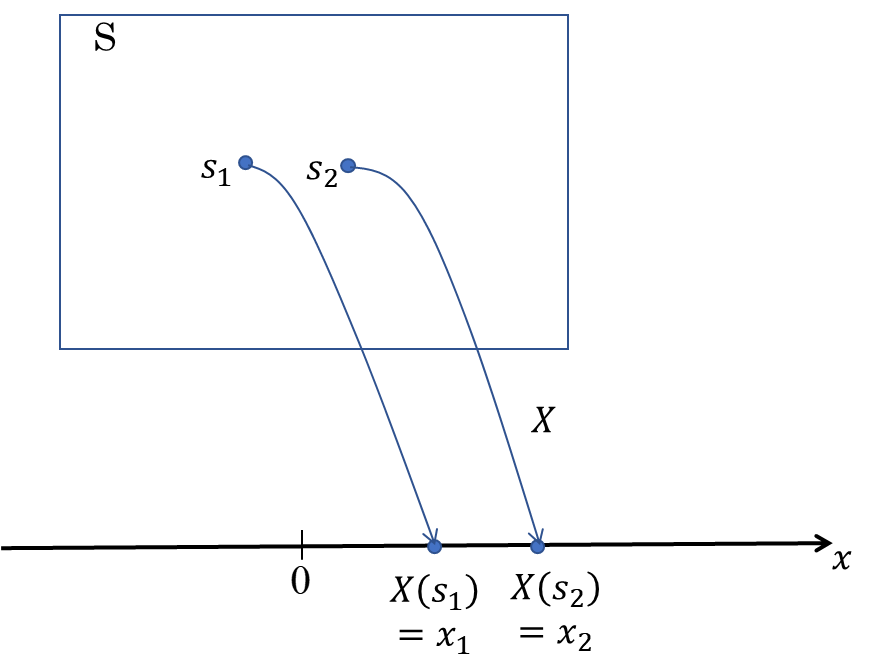
図3．確率変数：結果を数値で表す

 

例1．コイン投げの確率

2枚のコインを投げた時、表の出る確率を考えましょう。

 

標本空間は起こりうるすべての結果ですから、となります。コインに偏りがなければ、1/2の確率で表か裏が出ますから、

 

 

です。

 

確率変数を出た表の数と定義しましょう。すると、

 

 

確率変数がおのおのの値となる確率は、

 

 

となります。

 

なお、測量における確率変数は、観測値である基線ベクトル、距離、水平方向、水平角、高低角及び水準比高などです。

 

最近では、ネットワーク型RTK及び精密単独測位による座標値が確率変数として扱われています。

 

(注) 確率の定義は歴史的に、

(古典的定義) 同程度に確からしいn個の可能性があって、そのうちm個が事象Aを支持する結果だったとすれば、事象Aの確率は、

 

 

及び

 

(頻度による定義) 実験をn回繰り返して、ある事象Aに属する結果が出た頻度をとするとき、nを無限に大きくしていった時の相対頻度の極限をAの確率とする：

 

 

がありましたが、どちらも理論的には完全でない概念を含んでいるため（例えば、「同程度に確からしい」、極限の存在等）、現在は上で述べた公理的な確率の定義が採用されています。

 

（第２回 その２ 確率変数と確率分布 につづく）

3. 確率分布

確率分布は、確率変数の値とその値が出現する確率の関係を表したものです。

 

分布関数の定義：確率変数の値が以下となる確率を

 

 

と定義して、(累積)分布関数といいます。

 

分布関数の性質として、

 

 

が成り立ちます（図4及び図5参照）。

 

離散型の確率変数

確率変数が離散的な場合は、取り得る個々の値の確率が決まりますから、

 

 

を確率(密度)関数といいます。

 

例1のコイン投げの分布関数と確率関数を図4に示しました。

 

図4．累積分布関数と確率関数

 

連続型の確率変数

確率変数の累積分布関数が、関数によって次のように書けるとき

 

 

確率変数は連続であるといいます。は確率密度関数と呼ばれます(図5)。その時、確率変数がとの間の値をとる確率は、

 

 

と計算できます。これは、からまでの間での下の面積となります(図6)。

　もちろん、

 

 

なので、全区間におけるの下の面積は１となります。

 

図5．累積分布関数と確率密度関数

 

 

図6． ：影を付けた面積

 

4. 確率分布の指標

確率分布の特徴を表す指標として、特に重要なものが期待値と分散です。

 

期待値

期待値は英語のExpectationの頭文字で表示し、確率変数の値の(重み付き)平均として、次のように定義されます。

 

 

は、Xの取りうる値にその確率（重み）をかけて足したものです。一般にXの平均値とも呼ばれ、よく(ミュー)と書かれています。

 

分散

分散（Variance）は、確率変数の値のばらつきの度合いを示すものです。平均値とおいて、分散Vは

 

 

と定義されます。平均からのずれの二乗の平均です。和の形で表すと、

 

 

となります。計算には次の式が便利です。

 

 

また、分散の正の平方根を標準偏差と呼びます。多くの場合、標準偏差の値を(シグマ)、分散の値をと書きます。ただし、昔、標準偏差が独語の中等誤差(mittleren Fehler)の名称で使われていたことから、現在でも日本の公共測量作業規程の準則など多くの文献で、その頭文字であるmの記号を使っている場合があります。

参考文献

1． Koch, K-R., Parameter Estimation and Hypothesis Testing in Linear Models, Springer, 1999.

2． 東京大学教養学部統計学教室編: 統計学入門, 東京大学出版会, 2018.

 

次回は、いろいろな確率分布と計算例についてです。

 

（第3回 いろいろな確率分布 につづく）

2019年9月1日から2019年9月30日を有効期間とする

地殻変動補正提供サービス パラメータを生成しましたので、お知らせいたします。

 

パラメータの精度評価結果は以下の通りです。

水平方向の推定誤差の平均値は、   0.012 mです。

水平方向の推定誤差の標準偏差は、0.039 mです。

水平方向の推定誤差が4cm以下の地域の割合は、99.22％です。

 

なお、今回生成したパラメータは、すべての電子基準点のデータを使用し、

パラメータの生成および精度評価を行っています。

今後、パラメータと評価指標の精度向上のため、

解析条件を変更する可能性がありますので、予めご了承ください。

2019年8月1日から2019年8月31日を有効期間とする

地殻変動補正提供サービス パラメータを生成しましたので、お知らせいたします。

 

パラメータの精度評価結果は以下の通りです。

水平方向の推定誤差の平均値は、0.013 mです。

水平方向の推定誤差の標準偏差は、0.039 mです。

水平方向の推定誤差が4cm以下の地域の割合は、99.20％です。

 

なお、今回生成したパラメータは、すべての電子基準点のデータを使用し、

パラメータの生成および精度評価を行っています。

今後、パラメータと評価指標の精度向上のため、

解析条件を変更する可能性がありますので、予めご了承ください。