統計的推論では、データを確率変数の測定値（標本）としてモデル化することから始めます。それによりデータを生み出すメカニズムについて様々な結論を引き出すことができるからです。

 

今回は、統計的推論の手順と方法について簡単な例を交えて述べていきたいと思います（参考文献１）。

1．データ

データは、一般に二種類に分けられます。は確率変数の測定値、は既知の値として扱います。は被説明変数と呼ばれ、直接の測定値の場合もあれば、あらかじめ整理されている場合もあります（複数の観測の平均値や予備的解析の結果など）。は説明変数、独立変数などと呼ばれ、測定の条件を指定するもので確率変数としては取り扱いません。

 

なお、ここで変数やパラメータは一つの文字で書いていますが、一般に複数なのでベクトルと考えてください(例えば、)。

2．モデル

モデルとは、の(未知の)確率密度関数（母集団分布）を表すもので、次のように書けます。

 

 

ここで、はある形の確率密度関数で未知パラメータ(母数)を含みます。正確には、はパラメータの空間に属するのでモデルは確率密度関数の集まりということになります。はある集合(普通はある次元の実数空間)です。どのようなモデルを選択するかによって得られる結果は左右されますのでモデル選択は極めて重要です。ただ、基準点測量の場合、測定値の理論値は各基準点の位置から幾何学的に導かれますので、モデルの選択はあまり問題にはなりません。の期待値(平均)は、以下のように書けます。

 

(上式はを連続な変数として積分で書いていますが、離散変数の場合(和)も含んでいることにします。)

未知パラメータについては、をと分けて、今、関心のある（知りたい）パラメータとそうでない残りのパラメータに区別することもあります。を迷惑パラメータということもあります。もちろん何を知りたいかによって分け方も異なってきます。また、モデルによってはパラメータが完全に指定できない場合(母集団分布を完全に記述しない)もあります。

 

モデルの例

1)   正規分布の平均値（前回も参照のこと）

確率変数はおのおの独立で、未知の平均、既知の分散を持つ正規分布に従うものとします。この時、未知パラメータはということになります。もし、分散も未知なら未知パラメータはになります。平均値が知りたければ関心のあるパラメータはですが、目的によってはの時もあります。

 

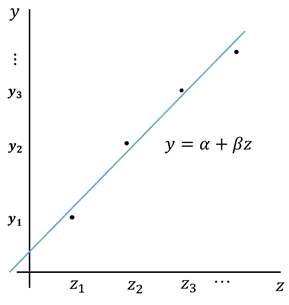
2)　線型回帰

データは個の組です。モデルは、

が独立で分散を持つ正規分布であり、

 

 

が成り立つとしたものです。つまり、観測値を(平均＋誤差)、

 

 

（誤差は正規分布に従うランダム誤差で分散は、平均は0）と考え、データの系統的な部分（期待値）の変動をに関する直線でフィットするものです(図1、図2)。傾きが知りたければ関心のあるパラメータは、迷惑パラメータはとなります。

 

3)   線型回帰一般化

　2)において、の確率分布の形を特定のものに仮定せず分散だけを与える場合があります。また、直線でなくの任意の関数でデータをフィットさせるようなモデルも考えられます。

 

図１．線型回帰

 

図2．線型回帰の意味（確率分布の平均値を直線フィットする）

 

4)   線形モデル

線型回帰モデルを多次元に一般化したもので、をベクトル、を既知の行列とすると、

 

が成り立つとするモデルです。ここで、は、の各成分の分散と共分散を成分に持つ分散共分散行列、は未知パラメータベクトル、は単位行列です。各成分は独立で正規分布に従うとします。はフルランクとします。3)と同じように誤差ベクトルを導入すると、

 

 

とも書けます。また、分散共分散行列は一般に

 

 

とすることも可能です。

また、3)と同じように一般化されたモデルを考えることもできます。

実は線形モデルの未知パラメータを解く方法が最小二乗法です。上記でベクトル・行列の性質と演算は定義や説明なしに書きましたが、最小二乗法を用いるために必要となりますので、次回以降、適宜補足して説明する予定です。

 

5)   非線形回帰

線形(あるいは一次)とは簡単に言うと直線関係ということですが、注意していただきたいことは、2)から4)で述べた線形モデルの本質は、と未知パラメータの関係が線形だということです。説明変数はデータとしては値の決まった係数ですから、式の中では(3)のように一次でもよいし3)で述べたように任意の関数でもよいのです。例えば、

 

 

とした場合でも、は値の決まった係数で、は未知パラメータに関して線形です。それに対し、(3)を非線形にした次のようなモデルを考えることができます。

 

 

この式は、未知パラメータに関して明らかに線形ではありません。さらに(4)を非線形にすると一般に次のような式になります。

 

 

ここで、はベクトルで、各成分は未知パラメータと説明変数に関する一般の非線形関数です。

 

6)　1)の一般化

1)は、がおのおの独立で、密度関数の分布に従うものと一般化できます。はある与えられた確率分布です。さらに、確率密度関数を、と仮定することもできます。は位置母数、は尺度母数といわれます。正規分布の場合は、位置母数は平均、尺度母数は標準偏差です。前回の正規分布の標準化と同様の考え方で、統計的性質は測定の単位や原点の位置に関わらず解析できるということを示しています。

 

7)   測量での例

測量における簡単な例を挙げておきましょう。

 

①   線形モデル：水準測量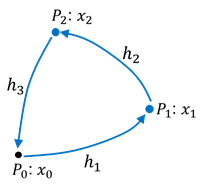

右図のような水準路線で、の標高を求める問題です。既知点の標高をとします。未知点の標高が未知パラメータ、確率変数の測定値が比高です。ランダム誤差ベクトル導入するとモデルは、

 

 

となります。右辺の誤差を除いた部分は未知パラメータの一次式になっていますので、線形モデルです（(6)の形）。

 

②    非線形モデル：距離観測による座標決定

右図のような距離観測によって未知点の平面座標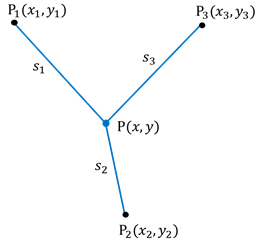を求める問題です。

未知パラメータは点の座標、各既知点からまでの平面距離が確率変数の測定値です。モデルは、

 

 

です。右辺の誤差を除いた部分は未知パラメータの関数ですが、二乗の和の平方根ですから明らかに線形ではありません（（9）の形）。この場合は、平方根の式を線形化してから解くことになります。

 

3.　推測の目的

統計的推測は、データを基に未知パラメータに関する情報や判断を評価するのが目的ですが、未知パラメータをどのように推測するかによって、おおきく点推定、区間推定、仮説検定の3つのタイプにわけることができます。

 

点推定：データからの推定量を求めること。

区間推定：の真の値を高い確率で含む区間あるいは集合を指定すること。

仮説検定：未知パラメータのある値に関する仮説を立て、データがそれを支持するかを検証すること。

 

他にも確率変数の予測や統計的決定理論さらにはモデルの選択の問題などがありますが、この連載の大きな主題である最小二乗法によるパラメータの推定は点推定に入ります。しかし、推定値を求めるだけでなくその信頼範囲を明示し検定を行う必要もありますので、上に述べた推測の主要な目的についてそれぞれお話しする予定です。

4．尤度と推定量の性質

推定量を求めることに関連した重要な概念をいくつか以下に示します。

4.1　尤度

尤度（ゆうど、もっともらしさ、英語ではlikelihood）とは、次のように定義される関数です。

 

 

ここでは確率密度関数‐を決めた時に測定値を得る確率‐なのでの関数ですが、尤度はが与えられたものとしての関数と見なすものです。尤度が大きいということは、観測されたデータを生み出すパラメータが真の値に近い可能性が大きいと考えても良いということです。そこで尤度が最大になるようなパラメータの値を求めて推定値とする方法を最尤推定法といいます。後にも述べますが、正規分布に対応した最尤推定法は最小二乗法と同値となります。

 

なお、計算上では対数をとった対数尤度が普通使われます。例えば、独立な個の測定値の同時確率分布は各分布の積なので尤度は、

 

 

となりますが、対数をとれば和となって扱いやすくなるからです。

4.2　不偏性

推定量の期待値が母集団の値と等しくなる時、それを不偏推定量といいます（前回も参照のこと）。つまり

 

 

ならば不偏です。不偏でなければ、0でない差（バイアス、偏り）

 

 

が存在します。

4.3　平均二乗誤差(Mean Square Error)

推定量の平均二乗誤差は、以下のように定義され、

 

 

推定量が平均して真値にどのくらい近いかの目安となります。書き換えると

 

 

つまり、分散とバイアス（の二乗）の和になります。

不偏推定量なら、 です。また、どの不偏推定量よりも分散が小さい推定量があるとき、それを最小分散不偏推定量といいます。

平均二乗誤差は、測量成果の品質評価の尺度として導入されています(前回の参考文献2参照)。

4.4　十分性

統計量とは推測に使われるデータ（確率変数）の関数でした（前回）。統計量があるパラメータの推測に使われる時、に関してデータから得られるすべての情報を含んでいれば十分統計量といい推測統計学における重要な概念です。例えば、平均値、分散とも未知の正規分布からの標本があるとします。この時、十分統計量は、

 

 

です。、はこれらの量から推定できるからです。

 

十分統計量がある場合、最尤推定量はその統計量の関数になること、さらに、上で述べた最小分散不偏推定量は十分統計量の関数に限られることも知られています。

5．二つの方法論

最後に統計的推測の方法論について簡単に触れておきます。現在2つの考え方があります。いわゆる古典的統計学と近年多用されるようになったベイズ統計学による推定です。二つの違いは、確率の考え方の違いから来ています。

 

従来の考え方では、確率分布を決める未知パラメータは未知ですがある真の値を持つとし、標本データから未知パラメータについての推測を行います。その意味では標本データがすべてであり、一回の観測でもデータが観測される確率は母集団から決まっています。

 

それに対し、ベイズ推定は未知パラメータも確率変数とする考えです。観測者が事前に持っている情報により未知パラメータもある確率(事前確率)で分布しており、それが測定データによって改訂され、より確からしい確率（事後確率）となるというものです。計算は高度で複雑になりますが、近年ではコンピュータ科学、生物学、医学、ビジネスなど様々な分野で使われるようになっています。この連載では古典的な推測を扱っていますが、機会があればベイズ推定にも触れたいと思います。

参考文献

1．Cox, D.R. : Principles of Statistical Inference (2006), Cambridge, Cambridge University Press.