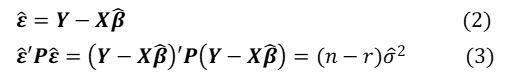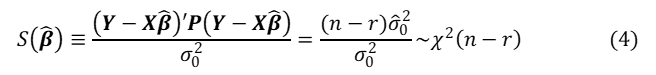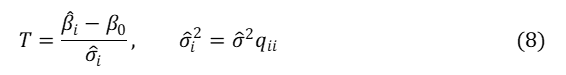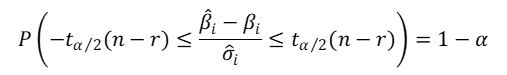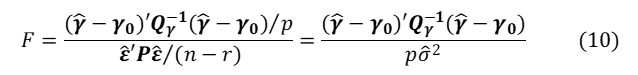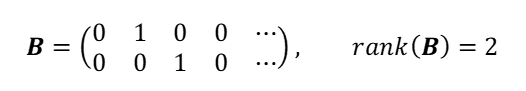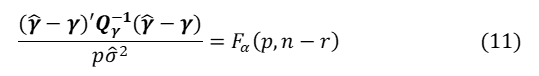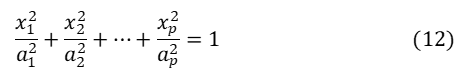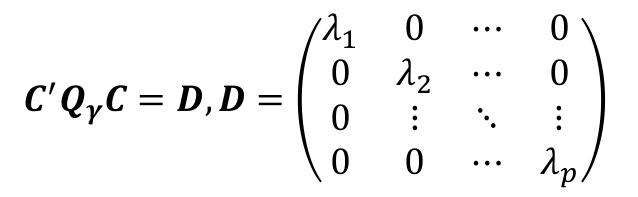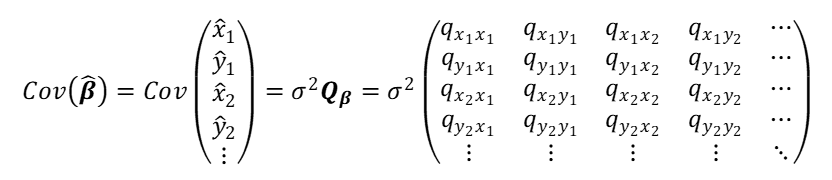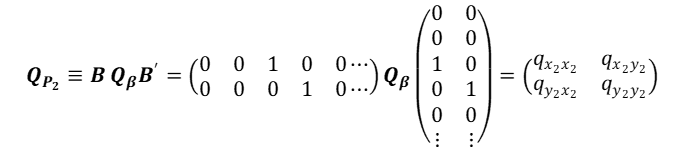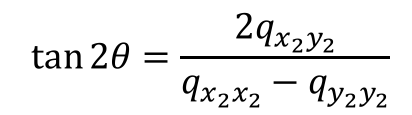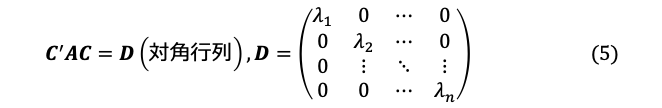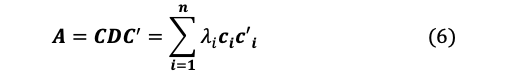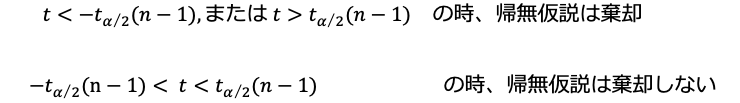2020年7月1日から2020年7月31日を有効期間とする

地殻変動補正提供サービス パラメータを生成しましたので、お知らせいたします。

 

パラメータの精度評価結果は以下の通りです。

水平方向の推定誤差の平均値は、 0.010 mです。

水平方向の推定誤差の標準偏差は、0.006 mです。

水平方向の推定誤差が4cm以下の地域の割合は、99.43％です。

 

なお、今回生成したパラメータは、すべての電子基準点のデータを使用し、

パラメータの生成および精度評価を行っています。

今後、パラメータと評価指標の精度向上のため、

解析条件を変更する可能性がありますので、予めご了承ください。

　最小二乗解が計算できると、残差、基準分散の推定値、解の誤差行列も得られますので、それらによりモデルも含めた最小二乗問題の評価をすることができます。ただし、具体的な計算をするためにデータの誤差は正規分布に従うと仮定します。

　今回は考え方と式を導き、具体的な計算例については次回ご紹介したいと思います。

１．残差と残差二乗和

　残差とその（重み付き）二乗和（第７，８回参照）

 

 

は、測定値と計算値の対応の良さを見る一つの目安となります。

　基準分散が既知の場合 は、残差二乗和を基準分散で割った量が自由度の分布（第5回）に従うことがわかっています。

 

 

この時、検定を行うことができます（付録B2）。

　最小二乗法によるあてはめに問題なければ、あるいはとなるはずなので、ここでは、帰無仮説を

 

 

対立仮説 を

 

 

として有意水準αで両側検定を行うことにしましょう。を計算し、

 

 

ならば、仮説は棄却されません。もし、棄却すべきとの結果になれば、測定値あるいはモデルに問題があるとして再検討しなければなりません。

　検定の例として、技術顧問中根勝見による以下の論文を挙げておきます：

 

日本の測地測量における統計検定の有用性についての数値的検証

(測地学会誌 第63 巻 第2 号 Journal of the Geodetic Society of Japan （2018）, 117-122 頁 Vol.63 , No 2, (2018), pp.117 -122）

2.　解の分散と誤差楕円

　最小二乗解とその共分散（誤差）行列は、次のように求められました（第７、8回）。

 

 

 

2.1 パラメータの検定と信頼区間

2.1.1　1つのパラメータの検定と信頼区間

　検定

　パラメータの一つ に注目し、帰無仮説 と対立仮説と対立仮説を

 

 

と設定して検定（がに等しいか否か）を行うことにします。このとき、統計量

 

 

は、自由度のt分布に従うことが分かっています。ここで、は基準分散の推定値、は

の成分で、は解の分散の推定値となります。従って、平均値の検定（B2）と同じように行うことができます。

 

 信頼区間

の信頼区間は、（真値）として

 

 

から

 

 

となります。

 

 2.1.2　複数のパラメータ

　F検定

　複数のパラメータを同時に検定する場合は、F検定を用います。帰無仮説は、

 

 

対立仮説は、

 

 

となります。帰無仮説は、 パラメータをある値に固定することに相当し、固定しない対立仮説との差をみるには、残差二乗和を比べ、次の統計量を計算します。

 

 

ここで、は最小二乗解の残差二乗和、はγに対応するの部分行列(注)で、分子はγの推定値と検定値との差の二乗和になっています。帰無仮説が正しいときに、Fは自由度のF分布に従うので、F検定を行うことができます。有意水準αとしてパーセント点を求め、

 

 

なら、仮説は棄却されます。対立仮説が正しいとすると、Fは差の二乗和で必ずある正数以上ですから、片側検定となります。

 

(注)と書け、Bは第j列から第k列までが単位行列をなし、他は0なのでランクはpとなり、は正定値で逆を持ちます（第8回A2参照）

例えば、とすると

 

 

で

 

 

です。

 

信頼領域と誤差楕円

　(10)において、有意水準をαとすれば、

 

 

この式はパラメータの信頼領域を表しており、パラメータの二次式ですから、を中心とした楕円体の形をしていることが分かります。

　楕円体の標準的な方程式は、

 

 

 なので、(11)をこの形に変換すれば楕円の大きさや軸の向きが分かります。そのために を直交行列Cで対角化（付録A3参照）：

 

 

して

 

 

とおくと、

 

 

となります。対角要素はの固有値、Cの列ベクトルは、各固有値に対応する固有ベクトルになります。

　従って、(11)は

 

 

を各軸の半径とする楕円体となります。Cの列ベクトルの方向が楕円体の軸の方向になります。

　特に、のとき、誤差楕円（体）と呼びます。従って、誤差楕円の各軸の長さは、です。

 

例．2次元の基準点測量

　未知パラメータは未知点の座標です。点 の誤差楕円を求めてみましょう。解の誤差行列を

 

 

と書くと、誤差楕円はに対応する行と列を取り出したの部分行列

から計算できます。計算の詳細は省略しますが、固有多項式を解いて（A3参照）、

 の固有値は、

 

 

また、に対応する固有ベクトルを とし、とx軸との角度をθとすると、

 

 

です。誤差楕円は図1のようになります。

 

図1．誤差楕円

 

 

 

 

 

 

 

A3.行列の演算２

 

　行列の固有値と固有ベクトル

　行列に対して

 

 

となるとき、をの固有値、をに属する固有ベクトルといいます。

　(1)が成り立つことは、となる があることなので、の列ベクトルは一次従属となり、は正則ではありません。したがって、その行列式は０、つまり

 

 

となります。

を固有多項式といい、に関して次の多項式です。 固有値は方程式(2)の根です。また、を に属する固有ベクトルとすれば、

 

 

となるので、固有ベクトルはスカラー倍してもよいことがわかります。

 

　対称行列に関して次が成り立ちます。

a.　の固有値 は実数。

b.   異なる固有値に属する固有ベクトルは、互いに直交する。同じ固有値に属する固有ベクトルは、

互いに直交するように選ぶことができる。

 

 

　ベクトルの正規化

　ベクトルの長さはですが、

 

 

は、と同じ向きを持つ長さ１のベクトルです。これをベクトルの正規化といいます。

 

　直交行列　

　行列 の列が、互いに直交し正規化されているとき、直交行列といいます。

直交行列 には、次の性質があります。

 

 

これは、を列ベクトルで

 

 

と書くと、の成分が

 

 

となることからわかります（第７回付録参照）。また、ベクトルに直交行列を掛けて

 

 

に変換すると、

 

 

より、変換されたベクトルの長さは不変なので、直交行列による変換は回転になることがわかります。

 

　対称行列の対角化

　対称行列に対して、直交行列が存在して、

 

　

 

となります。ここで、はの固有値、の列ベクトルは、固有値に属する正規化された固有ベクトルです。

　また、(5)を変形すれば

 

　

 

となります(スペクトル分解)。

 

B2. 仮説検定と区間推定

 

１．仮説検定

　検定と有意性

　検定（仮説検定）は、統計学において推定と並ぶ二つの柱の一つです。検定とは、母集団についての仮説をデータにもとづいて検証することです。観測結果が理論から期待される値と厳密に一致することはありませんが、その差が誤差の範囲なのか、それ以上に何か意味のあるものかを調べることになります。何か意味のあることを「有意」といい、仮説が有意か否かによって、仮説を棄却するか、あるいはしないかを決定することになります。有意の基準は確率で示され有意水準といい、 α で表すことが普通です。例えば α = 0.1( 10% ) とし、データが得られた確率が仮説に基づいて計算したところ 0.05( 5% ) となった場合、その仮説は棄却されます。

 

　帰無仮説と対立仮説

　仮説検定を確率分布とその母数（パラメータ）から見てみると、検定とは母数に関する仮説が正しいかをデータから決めることです。パラメータ θ の全体集合を Θ とすると、仮説  H0 とは、 θ が Θ の部分集合 Θ0 にふくまれること、 H0 : θ ∈ Θ0 と定義されます。H0 と対立する仮説 H1 ( H1 : θ ∉ Θ0 ) を立てることもあり、H0 を棄却するということは、H1 を採択することになります。 H0 を帰無仮説、 H1 を対立仮説といいます。帰無とは、最初に立てた仮説が無に帰る＝棄却される、という意味で、否定されることを期待することが多いので統計学ではそのような名前が付けられています。単に「仮説」として考えても問題ありません。

 

　片側検定と両側検定

　仮説検定の例として、平均値に関する検定を考えます。

ある量（長さ、温度、成分などn=10を回測って、

 

 

得たとします。母集団を

 

 

とし、このデータから μ = 18.0 であることを有意水準 α=0.05 で検定したいと思います。

 

帰無仮説は H0 :  μ = 18.0

対立仮説は H1 :  μ ≠ 18.0

 

です。

ここでは、母集団の分散が未知なので、次の統計量が従う自由度 n – 1 の t 分布（ 第5回 ）を利用した t 検定を行います。

 

 

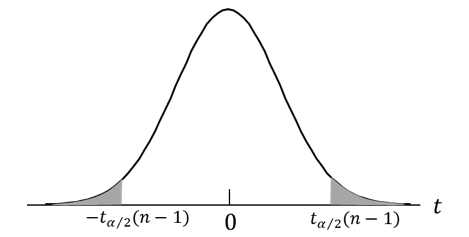
　t 分布は、図1のようになり、 の値がより小さいか、またはより大きい確率はαとなります。を α/2 パーセント点といいます（一般には小さいほうのパーセント点はですが、 t 分布は 0 を中心に左右対称なので、です。）

従って、

 

 

となり、仮説が棄却される値の領域を棄却域、棄却しない領域を採用域といいます。図1では、棄却域は両端の影がついた部分、採用域は中間部分です。

　この例では、t = -0.90 となり、α = 0.05 に対する α/2 パーセント点はですから、仮説は棄却しないことになります。また、棄却域は分布の両側にあるので両側検定といいます。

 

 

図1．両側検定

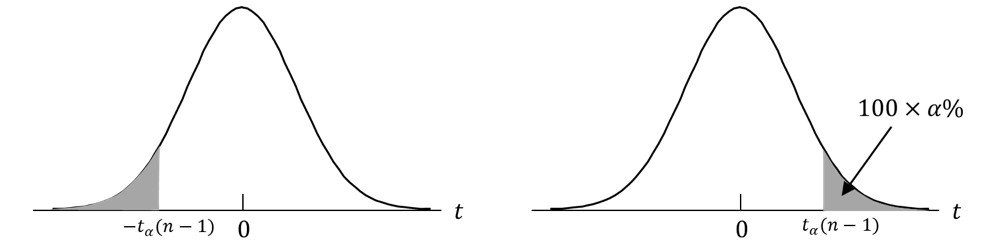
　もし対立仮説が、H1 : μ < 18.01 ならば、平均値が非常に小さくなった時にのみ帰無仮説を棄却することになるので α パーセント点はとなり、-1.83 < -0.90 なので帰無仮説は棄却されません。棄却域はとなり片側検定といいます。また、対立仮説の不等号を逆にすれば、棄却域はとなり、これも片側検定です。（図2）。

 

図2．左片側検定と右片側検定

 

　母分散に関する検定

　次の例として、母集団の分散に関する検定を考えます。連載5回によると

は自由度 n – 1 の分布に従うことがわかっています。平均値の検定と同じように、帰無仮説を、とし、有意水準で以下の対立仮説に応じて検定を行います。

1) なら両側検定で、なら H0 は棄却せず、それ以外は棄却。

2) なら左片側検定で、なら H0 を棄却、それ以外は棄却しない。

3) なら右片側検定で、なら H0 を棄却、それ以外は棄却しない。

これらを正規母集団の母分散に関する 検定といいます（図3）。

 

 

 図3．検定、両側（上）と片側検定

 

　F分布と分散の比に関する検定

　二つの確率変数 u と v が独立で、それぞれと に従うとき、その比 が従う確率分布を自由度( m, n ) のF分布 F(m,n) といいます(図4)。

 

図4．F分布

F分布は二つの正規母集団の分散について調べるときに使われます。二つの集団から得られた標本分散を、とすると(8)より、

 

 

ですから、

 

 

となり、F検定を行うことができます。

 

2．区間推定

　（点）推定は、未知パラメータ θ を一つの値として推定するものですが、区間推定は θが含まれるであろう区間（領域）をデータyによって推定するものです。式で書くと、θ が含まれる確率が 1 – α であるような区間、つまり

 

 

となる ( l( y ), u( y ) ) を求めることです。区間 ( l( y ), u( y ) ) を 100( 1 – α )% 信頼区間、l( y ), u( y ) を信頼限界といいます。1 – α は多くの場合、0.99 や 0.95 に選ばれます。信頼区間は、の標本分布から決められます。

 

　信頼区間の意味

　信頼区間はあるデータから計算され、データが違えばその値も変動します。パラメータの（真の）値は常数ですから、それが計算された信頼区間にある確率で含まれるということはありません。信頼区間が意味することは、同じ観測を何回も繰り返して信頼区間を計算したとき、θ を区間内に含む観測の割合が 1 – α であるということです。

 

　正規母平均の区間推定

　母集団の分散が未知のとき、(7)は t 分布に従いますから、

 

 

これをμについて解くと、

 

 

となり、μの 1 – α 信頼区間は

 

 

です。

　両側検定の例で使った結果の95パーセント信頼区間を求めてみましょう。

　n=10、平均値= 17.86、標本分散= 0.243、= 2.26 でしたから、95パーセント信頼区間は、

 

 

より、 ( 17.51, 18.21 ) となります。

 

B3. 正規分布の性質

　（多次元）正規分布をする確率変数の性質をまとめておきます。

 

　確率変数の独立性

　正規分布をしている確率変数ベクトルを のようにいくつかに分けたとき、対応する共分散行列も以下のように とブロックに分けられますが、

 

 

 

 

 ならば、 はおのおの独立になります（逆も真）。

 

　確率変数の線形関数

　( n × 1 ) ベクトルが正規分布をしているとき

 から線形変換で得られた ( m × 1 ) ベクトル

 

 

は、A のランクが m ならば正規分布に従います。

 

 

 

例．最小二乗解の誤差分布

　最小二乗解

 

 

は、データの線形変換 のランクは  ですから、 が正規分布、

 

 

ならば、 も正規分布で より

 

 

となります。

 

　確率変数の和

　( n × 1 ) ベクトル が独立で、正規分布 に従うとき

　( n × 1 ) ベクトルも正規分布となります。

 

 

ここで、 です。

 

参考文献

1. Koch, K-R., Parameter Estimation and Hypothesis Testing in Linear Models, Springer, 1999.