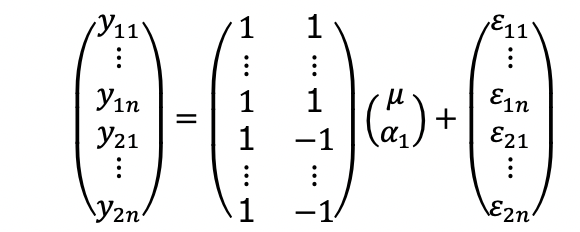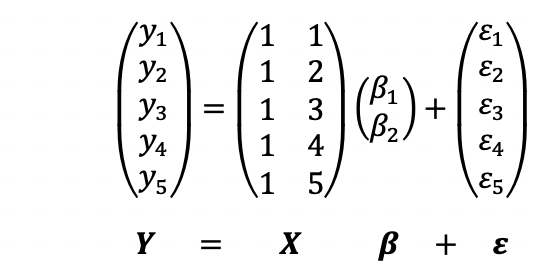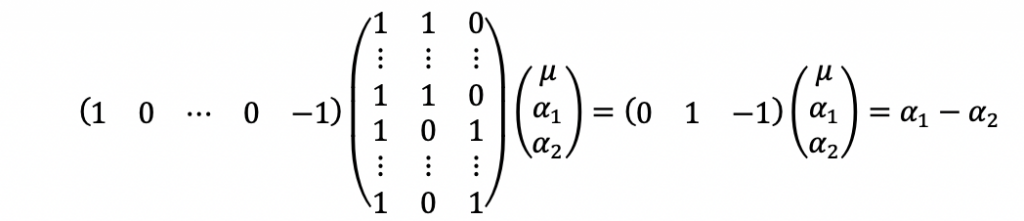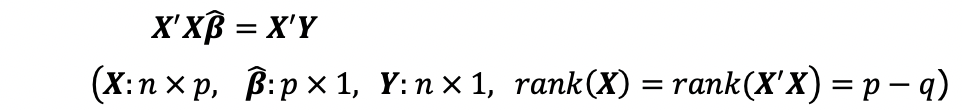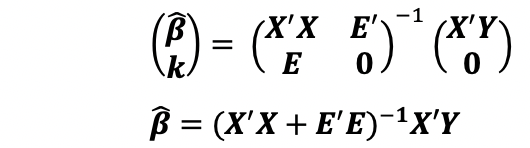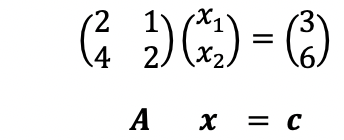パラメータ情報
【地殻変動補正提供サービス】パラメータの生成と評価:2020年12月1日~12月31日
2020年11月30日
2020年12月1日から2020年12月31日を有効期間とする
地殻変動補正提供サービス パラメータを生成しましたので、お知らせいたします。
パラメータの精度評価結果は以下の通りです。
水平方向の推定誤差の平均値は、 0.010 mです。
水平方向の推定誤差の標準偏差は、0.006 mです。
水平方向の推定誤差が4cm以下の地域の割合は、99.44%です。
なお、今回生成したパラメータは、すべての電子基準点のデータを使用し、
パラメータの生成および精度評価を行っています。
今後、パラメータと評価指標の精度向上のため、
解析条件を変更する可能性がありますので、予めご了承ください。
実験結果レポート
CLAS補強対象衛星に関する事前調査(2020.11)
2020年11月18日
※本資料は、2020年11月18日にQBIC(高精度衛星測位サービス利用推進協議会)主催で開催された第7回社会実装推進WG(拡大会議)で利用した資料です。
CLASの補強対象衛星が11機から17機に引き上げられることを受け、どの様な効果があるかを検証するために、フィールドテストを行いました。
本調査は、事前実証用の仕組みを利用して検証したものであり、実際のサービス、受信機等とは異なるため、参考試験となります。
また、サービス開始前の調査には、多くのご協力をいただきましたので、改めて謝辞を述べさせていただきます。
*今回の実験で利用した「GNSS-Explorer」,「SARVAL」についてはこちらで紹介しています。
誤差論と最小二乗法
第11回 最小二乗法に関するいくつかの補足
2020年11月20日
今回は、線形モデルの最小二乗法による推定について少し一般的な事柄を述べておきたいと思います。また、モデルを選択する場合の基準について紹介します。
1.推定可能性と最小二乗推定値
1.1 ランク落ちのモデル
標準の線形モデル、
において、Xのランクがpより小さい(ランク落ち)場合があります。そのまま、正規方程式をたてるとX’X(p×p行列)が逆行列を持たないため、一意の解を求めることはできません。
例えば、一元配置モデルといって、実験結果に影響を及ぼす因子があり、因子のレベルを変えて効果を調べることがあります。
レベルを変えた効果を調べるために
というモデルを考えます。 μは全体の平均値、![]() はレベル1の効果、
はレベル1の効果、![]() はレベル2の効果を表しています。それぞれn 回の測定をしたとすると、観測方程式は、
はレベル2の効果を表しています。それぞれn 回の測定をしたとすると、観測方程式は、
となりますが、Xのランクは2(第2列と第3列を足すと第1列になる)でありランク落ちしています。
この場合、すべてのパラメータを解くことはできませんが、いくつかの方法で解決することができます。
a)モデルを見直して、一意に決まるパラメータを選ぶ。
b)パラメータに条件を付けくわえる。
c)一意に決まるパラメータの線形式を作って推定する。
等です。
例えば、
となり、観測方程式は
となります。 Wはフルランク(rank=2) なので、正規方程式で解けます。
b)例えば、
という条件を付けると、
なので、
となり、これも解けます。
ただし、この場合はパラメータの定義(意味)が変更されることになるので注意が必要です。
c)一意に決まるパラメータの線形式(推定可能関数、次節参照)は解けます。
例えば、
等は、一意に推定可能です。
1.2 推定可能性
ここで、線形モデル
における未知パラメータの推定について、少し詳しく見ていきたいと思います。
一般に(線形とは限らず)、 E(Y)をパラメータ![]() の関数で表したものがモデルです。
の関数で表したものがモデルです。
となることが条件となります。これは、![]() が
が![]() の関数であることと同じで、そうでなければデータ(の期待値)E(Y)によって
の関数であることと同じで、そうでなければデータ(の期待値)E(Y)によって![]() を推定することができません。線形モデルに限ると、
を推定することができません。線形モデルに限ると、
であれば、一意に決められることになります。これを推定可能と言っています。
例1.直線回帰のモデル(第7回)
において、
パラメータの推定可能条件
線形モデルを、
と Xの列ベクトルの一次結合で表すと、未知パラメータ ![]() が推定可能でない条件は、
が推定可能でない条件は、
となる ![]() が存在すること、つまり
が存在すること、つまり![]() が他の列ベクトルの一次結合となることです。
が他の列ベクトルの一次結合となることです。
推定可能性と不偏性
推定値が不偏とは、期待値が真値に等しくなることで、 ![]() をパラメータの関数
をパラメータの関数![]() の推定値とするとすべての
の推定値とするとすべての![]() に関して
に関して![]() となります。これから、
となります。これから、![]() の線形関数
の線形関数![]() が推定可能
が推定可能![]() (不偏)となる推定値
(不偏)となる推定値![]() があることがわかります。
があることがわかります。
1.3 最小二乗推定値
最小二乗解は、幾何学的に考えると次の式を満たすものです(第7回参照)。
ここで![]() は
は![]() への直交射影(図1)を与える行列で、
への直交射影(図1)を与える行列で、![]() を
を![]() に直角に射影した
に直角に射影した![]() との距離が0になるような
との距離が0になるような![]() をあたえる
をあたえる![]() が最小二乗解でした。
が最小二乗解でした。
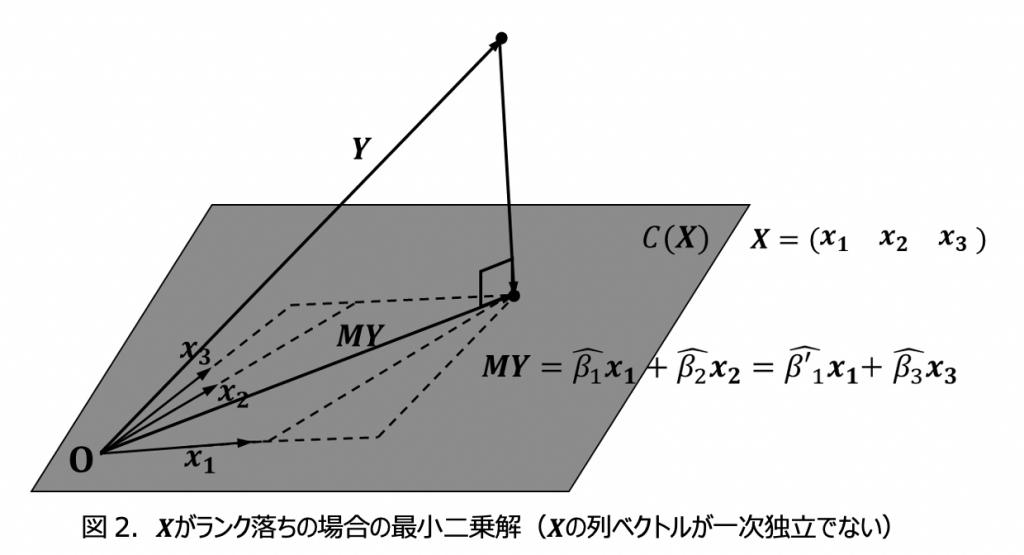
一般には Xがランク落ちしていても、直交射影は定義され、その行列は一般逆行列(付録参照)を用い、
と書かれます。 Xがランク落ちしているときは、![]() は一意には決まりません(図2)。
は一意には決まりません(図2)。
ただし、直交射影は一意であり、推定可能関数は![]() の線形式でしたから、推定可能関数の最小二乗解は一意に決まることがわかります。つまり、推定可能関数
の線形式でしたから、推定可能関数の最小二乗解は一意に決まることがわかります。つまり、推定可能関数![]() の一意な最小二乗解は、
の一意な最小二乗解は、
です。
Gauss-Markovの定理(第7回)は、推定可能関数の最小二乗解についてそれがBLUE(最小分散の不偏な線形の推定値)であることを示しています。
例2.自由網平均
測地網はそれを構成する基準点の座標を決定することによって構築されます。普通は、複数の固定点あるいは1点及び1方向を決めて、最小二乗法による平均計算を行います。ただし、点の位置の変動などを求めたい時に全点を未知点とする場合があります。そのような平均計算を自由網平均と呼びます。自由網平均では、網の位置、方向が不定となりますので、計画行列はランク落ちになり、標準的な最小二乗法では一意に解けません。そのため、何かしらの条件を付けるのですが、解のノルムが最小になるという条件を付けるのが自由解です。自由解は、正規方程式、
付録にある通り、最小ノルム解は必ず一つ存在するので、
として自由解が求まることになります。
もう一つの解法として、![]() に特別な拘束条件を付けて解く方法があります。
に特別な拘束条件を付けて解く方法があります。
最小ノルム解![]() は一般解の
は一般解の![]() 成分なので、Xの零空間の成分はありません。従って、零空間の基底となるベクトルを列とする
成分なので、Xの零空間の成分はありません。従って、零空間の基底となるベクトルを列とする![]() 行列
行列![]() があれば、
があれば、
となります。この結果、線形モデルは拘束条件が付いて
となります。詳細は略しますが、拘束条件がある最小二乗法の正規方程式は拡張された形、
と解くことができます。もちろん![]() は、擬逆行列による解と一致します。
は、擬逆行列による解と一致します。
2.モデルの選択とAIC
統計的推定において、実はモデルの選び方は大変重要な問題です。ここでは、モデルの妥当性を判断する基準として有名なAIC(Akaike’s Information Criterion: 赤池の情報量基準)を紹介します。
我々が測定したデータは、真のモデル(母集団)から得られるものと考え、データを最もよく記述するモデルを知ることがパラメータ推定の目的です。最もよいモデルとは真に近いということですから、真のモデルとの差を何らかの量として表し、それが最小になるようなモデルを選べばよいということになります。詳細は省きますが、真のモデルとの差はKullback-Leibler情報量![]() として知られているものがあります。
として知られているものがあります。
真の確率分布はわかりませんが、最尤推定値から![]() を推定できることが赤池によって示されました。AICは(定数倍と定数を除いた)その推定量で、小さいほど良いモデルということができます。
を推定できることが赤池によって示されました。AICは(定数倍と定数を除いた)その推定量で、小さいほど良いモデルということができます。
最小二乗法におけるAICは、データの正規分布を仮定して
となります。ここで![]() :データ数、
:データ数、![]() :推定パラメータ数、
:推定パラメータ数、![]() 残差です。
残差です。
参考文献
- Christensen, R.: Plane Answers to Complex Questions: The Theory of Linear Models, Fifth Edition (2020), Springer Texts in Statistics, New York.
- Koch, K-R., Parameter Estimation and Hypothesis Testing in Linear Models (1999), Springer.
- Burnham, K.P. and Anderson, D. R.: Model Selection and Multimodel Inference, Second Edition (2002), Springer, New York.
誤差論と最小二乗法
第11回付録
一般逆行列
一般逆行列は、逆行列の考えを拡張したもので次のように定義されます。
となる![]() 行列
行列![]() を
を![]() の一般逆行列といい
の一般逆行列といい![]() と書きます。一般逆行列は一意には決まりませんが、
と書きます。一般逆行列は一意には決まりませんが、![]() が正則の時は、
が正則の時は、![]() (一意)となります。
(一意)となります。
すべての行列に関してその一般逆行列が存在します。特に![]() が対称行列とすると、
が対称行列とすると、![]() は直交行列
は直交行列![]() と対角行列
と対角行列![]() (
(![]() は対角要素)が存在して、
は対角要素)が存在して、
と分解できる(特異値分解)ので
は、一般逆行列です。
例1.
直交射影行列
一般逆行列を使うと、ベクトルの![]() (
(![]() の列ベクトルが作る空間)への直交射影を与える行列は、
の列ベクトルが作る空間)への直交射影を与える行列は、
と書けます。この行列は、対称行列になっています。
一次方程式の一般解と最小ノルム解
一次方程式
が解を持てば(第8回付録参照)、
となるので、
は(4)の解になります。解はただ一つの場合も無限にある場合もあり、一般解は、
です。
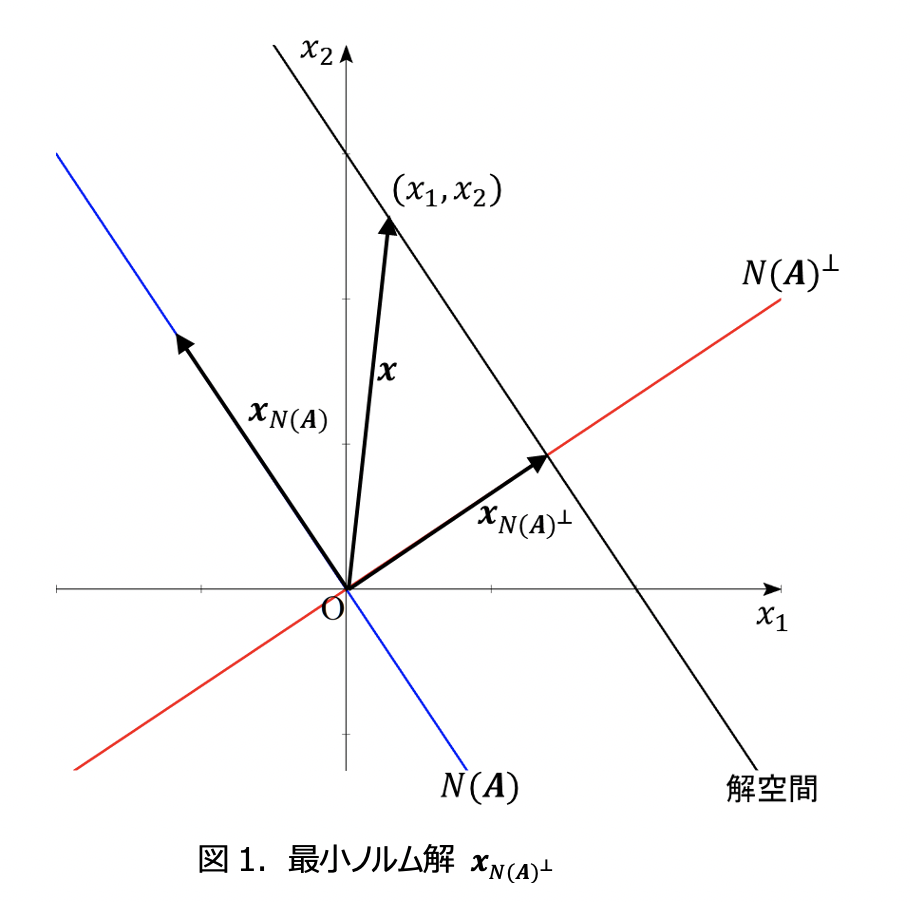
しかし、ノルム(長さ)が最小になる解に限ると、その解は一意に決まることが分かっています。概略は以下の通りです。
一次方程式の一般解は、一意に2つの直交する成分に分けることができます。
ここで、![]() は
は![]() となる空間(零空間)で
となる空間(零空間)で![]() はそれに直交する空間です。
はそれに直交する空間です。![]() は、
は、![]() の解で無限にありますが、
の解で無限にありますが、![]() は一つしかありません。((6)を見ると、一般解はある一つの解に
は一つしかありません。((6)を見ると、一般解はある一つの解に![]() の解を加えたものになっていることが分かります。)
の解を加えたものになっていることが分かります。)
また、各成分は直交するので
となり、![]() は最小のノルムを持つことが分かります。この最小ノルム解を行列を用いて
は最小のノルムを持つことが分かります。この最小ノルム解を行列を用いて
と書くと、![]() は擬逆行列と呼ばれているものになり一意に決まります。
は擬逆行列と呼ばれているものになり一意に決まります。
擬逆行列は一般逆行列を用いて
と表されることがわかっています。
行列の列ベクトル空間と零空間
また、
例2.一次方程式の最小ノルム解
一次方程式
参考文献
- Koch, K-R., Parameter Estimation and Hypothesis Testing in Linear Models (1999), Springer.