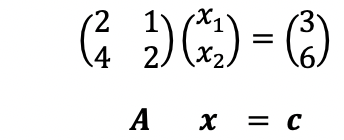一般逆行列

一般逆行列は、逆行列の考えを拡張したもので次のように定義されます。

行列に対して

 

となる行列をの一般逆行列といいと書きます。一般逆行列は一意には決まりませんが、が正則の時は、（一意）となります。

すべての行列に関してその一般逆行列が存在します。特にが対称行列とすると、は直交行列と対角行列（は対角要素）が存在して、

 

と分解できる（特異値分解）ので

 

は、一般逆行列です。

例１．

とすると、（cは任意）は一般逆行列です。

 

直交射影行列

　一般逆行列を使うと、ベクトルの（の列ベクトルが作る空間）への直交射影を与える行列は、

と書けます。この行列は、対称行列になっています。

 

一次方程式の一般解と最小ノルム解　

　一次方程式

が解を持てば（第8回付録参照）、

なので、

となるので、

は(4)の解になります。解はただ一つの場合も無限にある場合もあり、一般解は、

です。

しかし、ノルム（長さ）が最小になる解に限ると、その解は一意に決まることが分かっています。概略は以下の通りです。

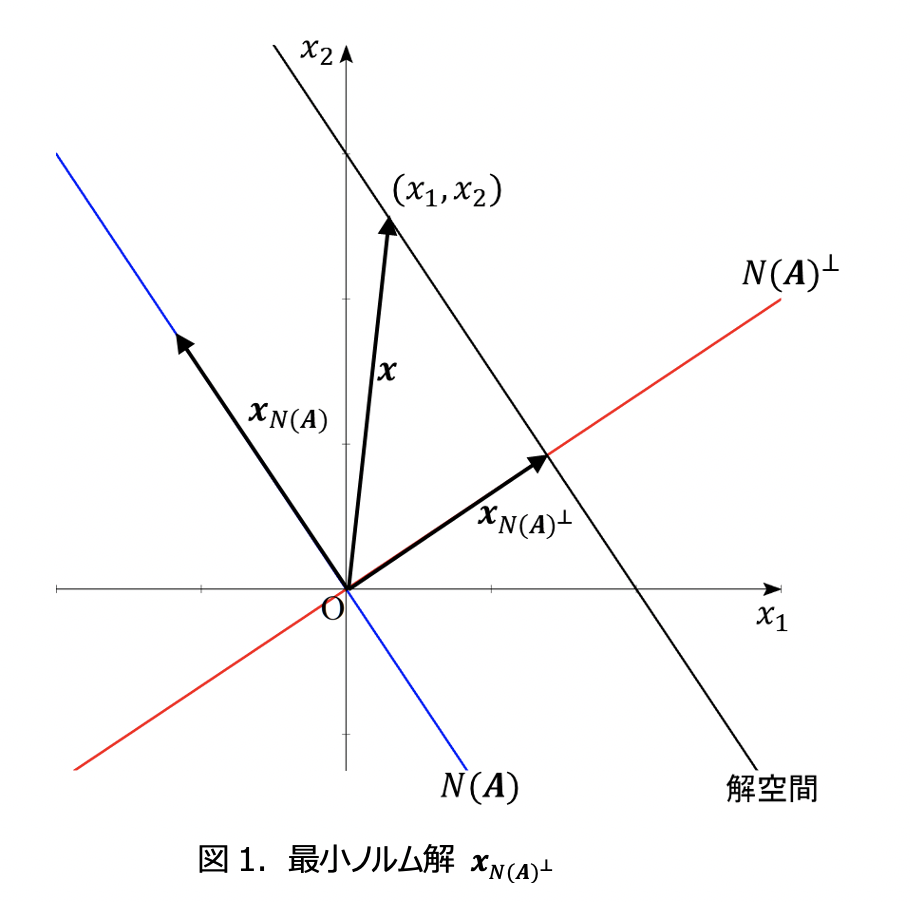
一次方程式の一般解は、一意に2つの直交する成分に分けることができます。

 

ここで、はとなる空間（零空間）ではそれに直交する空間です。は、の解で無限にありますが、は一つしかありません。（(6)を見ると、一般解はある一つの解にの解を加えたものになっていることが分かります。）

また、各成分は直交するので

 

となり、は最小のノルムを持つことが分かります。この最小ノルム解を行列を用いて

 

と書くと、は擬逆行列と呼ばれているものになり一意に決まります。

擬逆行列は一般逆行列を用いて

 

と表されることがわかっています。

 

行列の列ベクトル空間と零空間

行列の列ベクトルからなる空間を（第7回付録）と書きました。

零空間は、となるベクトルの空間です。以下の関係があります；

の直交補空間（の中でと直交する空間）をとすると、

とすると（dimは次元の数）、

また、

 

例2．一次方程式の最小ノルム解

　一次方程式

 

 

 

を考えましょう。のランクは1で、解は

 

をみたすとなります。は直線、は直線です。

最小ノルム解は、成分のとなります。

 

参考文献

1. Koch, K-R., Parameter Estimation and Hypothesis Testing in Linear Models (1999), Springer.