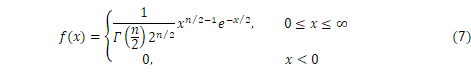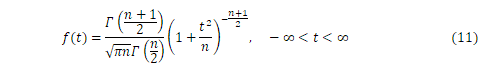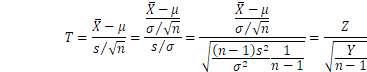ナレッジ
第5回 その1 – 統計的推論
2019年11月06日
確率分布を取り扱う確率論は数学理論ですから、確率分布が与えられればそれに従う確率変数の振る舞いを数学的に厳密に解析することができます。私たちが取り扱う現実の問題では、観測して集めたデータや測定値(確率変数)は何らかの確率分布に従っている集団(母集団)からの標本(サンプル)と考えられます。私たちが知りたいのは、多くの場合データそのものではなく、データが持つ普遍的な性質、データが表す社会的動向や科学的真実です。つまりデータが属する母集団のパラメータ・性質ということになります。しかし、母集団を完全に知ることは困難な場合が多いので、持っているデータを用いて「推定」を行うことになります。その統計学的方法を推測統計学 (統計的推測)といいます。
1.記述統計学から推測統計学(統計的推測)へ
統計学は19世紀後半から20世紀初頭にかけて発展し、現在の統計学でも使われる基礎的概念が完成しました。観察されたデータを整理・要約しその集団的性質を明らかにする手法で記述統計学と呼ばれます。しかし、当時の統計学は標本の数を多くすれば真実に近くなるという大標本を前提とした理論で、データの背後にある母集団という概念は意識されていませんでした。その後20世紀に入って、集団全体を調べることができない場合でも部分的に選ばれたデータを分析して元の集団を推測するという統計的推測の方法が確立されました(参考文献1)。
測量・測地学の分野については、以下、参考文献2から引用しておきます。
「しかし,推測統計学は直ちに測地学へ導入されたわけでなく,統計的仮説検定が,本格的に測地学の論文及び教科書に使われるようになったのは,20世紀後半になってからである。とりわけ計算量の多い測地学では,電子計算機の実用化が不可欠であった。世界的には,現在の測位・測量成果の品質管理の誤差論に使われている。我が国の測量分野では,現在においても統計的仮説検定のような推計統計学の成果は,使われてない。」
2.標本分布
標本分布は確率論と統計的推測を結び付けるものです。確率変数である標本から作られた統計量の確率分布を決めることは統計的推測の重要なステップです。
標本と母集団については連載第1回でもふれましたが、基本的な概念をもう一度定義から述べたいと思います。
母集団:これから調べたいと思うすべての対象あるいは測定値の集まり。
一般に母集団は確率分布を持つと考えられ、それを母集団分布といいます。母集団分布は未知なことが普通です。母集団は有限の場合もありますが、測量などの測定値の場合は無限と考えるのが普通です。
標本(サンプル):観測可能な確率変数の組、![]() 。
。![]() を標本の大きさという。
を標本の大きさという。
ランダムサンプル:各確率変数が独立で同じ確率分布に従う場合の標本。
標本がランダムの場合、次に定義される統計量の計算が簡単になりますので、以下特に断らない限りランダムサンプルを扱います。
母集団の推測に使われるもので、標本平均や分散などは統計量の例です。統計量は確率変数の関数なので、当然確率変数となります。例えば、標本平均![]() は確率変数
は確率変数![]() の関数なのでやはり確率変数で、標本によってその値がばらつきます。従って、確率分布を持ちます。
の関数なのでやはり確率変数で、標本によってその値がばらつきます。従って、確率分布を持ちます。
標本分布:統計量の確率分布のこと。
次に例を示しましょう。
例1.標本平均の確率分布
簡単のために5個の有限母集団を考えます。母集団が数値![]() からなるとします。これから3つを選んだ標本をすべて調べましょう。標本の選び方は、
からなるとします。これから3つを選んだ標本をすべて調べましょう。標本の選び方は、![]() 通りありますから、それぞれ平均をとって表にすると、
通りありますから、それぞれ平均をとって表にすると、
表を見ると、例えば![]() あるいは
あるいは![]() の標本では平均値
の標本では平均値![]() が
が![]() になり、これが標本から母集団平均を推定した値です。平均値が
になり、これが標本から母集団平均を推定した値です。平均値が![]() となる標本は10個のうち2つですから、その確率は
となる標本は10個のうち2つですから、その確率は![]() となります。このように平均値は標本によってばらつきますので、確率的な取り扱いが必要になります。
となります。このように平均値は標本によってばらつきますので、確率的な取り扱いが必要になります。
ここでいくつか重要な式を導いておきたいと思います(連載第1回も参照)。
平均![]() 、分散
、分散![]() の母集団から抽出した大きさ
の母集団から抽出した大きさ![]() の標本を
の標本を![]() とします。
とします。
標本平均の期待値
つまり、標本平均の期待値は母集団平均に等しくなります。
標本平均の分散
となり、母集団分散の![]() になります。
になります。![]() が大きくなると分散が0に近づきますから、
が大きくなると分散が0に近づきますから、![]() (標本平均)→
(標本平均)→ ![]() (母平均)になることが証明されます(大数の法則)。
(母平均)になることが証明されます(大数の法則)。
標本分散の期待値
第1回で標本分散を定義しました。
この期待値を計算してみましょう。![]() (連載第2回参照)を使うと、
(連載第2回参照)を使うと、
従って標本分散の期待値は母集団分散と等しくなります。
標本平均や標本分散のように期待値が母集団のものと一致することを「不偏」(平均的に過少でも過大でもなく正しい)といいます。その意味で、標本平均や標本分散は不偏推定量になっています。標本分散の場合は確率分布の定義から で割った分散を使うと不偏ではなくなるので注意が必要です。 が大きい場合はその差はほとんどありませんが、10以下ですと10%以上の差になります。
(第5回 その2 統計的推論 につづく)
参考文献
1.蓑谷千凰彦(1995):推定と検定のはなし、東京図書.
2.中根勝見(2018):日本における誤差論の歴史的考察、写真とリモートセンシング Vol.57.No4、152-159. または、アイサンテクノロジー株式会社 Website
https://atmsp.aisantec.com/atmspark/modules/IA_34/index.php?id=12
3.Ramachandran, K.M. & Tsokos, C.P.: Mathematical Statistics with Applications (2009), Elsevier Academic Press.
ナレッジ
第5回 その2 – 統計的推論
3.正規分布からの標本
この項では特に母集団が正規分布からの標本分布を考えます。正規分布は第3回に述べたように統計学における基本の分布ですから、ここで導かれる統計量はさまざまな場面で活用される重要なものです。
正規分布は次の重要な性質をもっています。
(i)正規確率変数の線型変換は正規確率変数: ![]() が正規分布
が正規分布![]() に従うとき、
に従うとき、![]() は正規分布
は正規分布![]() に従う。
に従う。
(ii)独立な正規確率変数の和は正規確率変数:![]() を独立な確率変数とし、各
を独立な確率変数とし、各![]() は平均
は平均![]() 分散
分散![]() を持つ正規分布に従うとする。その時、
を持つ正規分布に従うとする。その時、![]() の分布は、平均
の分布は、平均![]() 、分散
、分散![]() の正規分布となる。
の正規分布となる。
つまり独立で正規分布に従う確率変数は、和や差をとったり定数倍しても再び正規分布となるのです。
例えば、測量において、距離、方向及び比高などあらゆる観測値を標準偏差で割った標準化変数![]() を使うことによって、こうした異種観測値が同時網平均できることになります。
を使うことによって、こうした異種観測値が同時網平均できることになります。
3.1 標本平均の分布-分散が既知の時
正規母集団の平均と分散をそれぞれ![]() 、
、![]() とすれば、標本平均は
とすれば、標本平均は![]() ですから(ii)を適用して(
ですから(ii)を適用して(![]() とすればよい)、
とすればよい)、
これは、一つのものを繰り返し観測した場合、推定値の精度を2倍にしたければ観測数は4倍にしなければならないことを示しています。
標本分散は、
ですから、その分布を知るためには確率変数の二乗和が従う分布が必要になります。正規分布に従う確率変数の二乗和の分布が![]() (カイ二乗)分布です。
(カイ二乗)分布です。
確率変数![]() が、
が、![]() を正の整数として次の形の確率密度関数を持つとき、自由度
を正の整数として次の形の確率密度関数を持つとき、自由度![]() の
の![]() (カイ二乗)分布
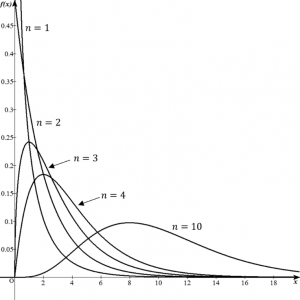
(カイ二乗)分布![]() といいます(図1)。
といいます(図1)。
ここで、![]() はガンマ関数という関数で、
はガンマ関数という関数で、![]() のとき、
のとき、![]() が成り立ち、
が成り立ち、![]() という値をとります。
という値をとります。
さて、![]() を正規母集団
を正規母集団![]() からのランダムサンプルとします。これを標準化して
からのランダムサンプルとします。これを標準化して![]() とすると各
とすると各![]() は標準正規分布の確率変数となります。この時、それらの二乗和
は標準正規分布の確率変数となります。この時、それらの二乗和
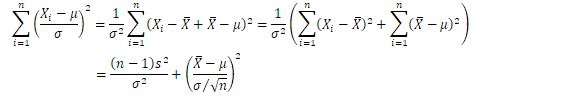
と変形すると、左辺は自由度![]() の
の![]() 分布、右辺第2項は自由度1の
分布、右辺第2項は自由度1の![]() 分布を持ちます。このことと(詳しい証明は省きますが)
分布を持ちます。このことと(詳しい証明は省きますが)![]() と
と![]() が独立なことから、右辺第1項が自由度
が独立なことから、右辺第1項が自由度![]() の
の![]() 分布に従うことがわかります。つまり、
分布に従うことがわかります。つまり、![]() を正規母集団からの標本分散としたとき統計量、
を正規母集団からの標本分散としたとき統計量、
は自由度![]() の
の![]() 分布に従います。これを使えば、標本分散から母分散について統計的推論を行うことが可能になります。また、後に述べる最小二乗法では残差の二乗和に対して
分布に従います。これを使えば、標本分散から母分散について統計的推論を行うことが可能になります。また、後に述べる最小二乗法では残差の二乗和に対して![]() 分布を用いて検定を行います。
分布を用いて検定を行います。
3.3 標本平均の分布-分散が未知の時:t分布
3.1で母集団の分散が既知ならば標本平均![]() の分布は正規となり、
の分布は正規となり、![]() は標準正規分布に従うことを見ましたが、一般的には母集団の分散は未知です。その場合、母分散の代わりに標本分散を使うことが考えられます。標本のサイズが大きい時は
は標準正規分布に従うことを見ましたが、一般的には母集団の分散は未知です。その場合、母分散の代わりに標本分散を使うことが考えられます。標本のサイズが大きい時は![]() と仮定でき中心極限定理により
と仮定でき中心極限定理により![]() が近似的に
が近似的に![]() に従うことがわかります。しかし、標本が小さい場合この仮定は使えず、
に従うことがわかります。しかし、標本が小さい場合この仮定は使えず、![]() は(スチューデントの)t分布というものになることが知られています。t分布は、小標本
は(スチューデントの)t分布というものになることが知られています。t分布は、小標本![]() の場合に有用な分布です。
の場合に有用な分布です。
(スチューデントの)t分布
![]() と
と![]() が独立の確率変数で、
が独立の確率変数で、![]() が自由度
が自由度![]() の
の![]() 分布、
分布、![]() が
が![]() に従うとします。その時、確率変数、
に従うとします。その時、確率変数、
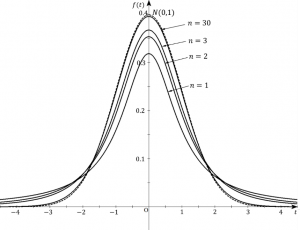
になります(図2)。t分布は左右対称なので平均は0、また、![]() なら分散は
なら分散は![]() です。
です。![]() が大きくなるとt分布は標準正規分布に収束することが証明されており、図2からもわかるように
が大きくなるとt分布は標準正規分布に収束することが証明されており、図2からもわかるように![]() が30以上では標準正規分布で近似しても問題ありません。
が30以上では標準正規分布で近似しても問題ありません。
正規母集団からのランダムサンプルの場合、次が成り立ちます。
大きさ![]() の標本平均と分散をそれぞれ
の標本平均と分散をそれぞれ![]() 、
、![]() 、母集団平均と分散をそれぞれ
、母集団平均と分散をそれぞれ![]() 、
、![]() とすると統計量、
とすると統計量、
なぜなら、
となって、![]() と
と![]() が独立なことから
が独立なことから![]() と
と![]() も独立になり、t分布
も独立になり、t分布![]() に従う統計量の定義(10)に合致するからです。
に従う統計量の定義(10)に合致するからです。
t分布は、正規分布の代用とも考えられますが、小標本の場合の厳密な確率分布です。図2を見ると正規分布はt分布よりピークがとがっています。そのため小標本の場合、正規分布を使うと平均からはずれる確率を過小評価していることになります。
例えば、2回の観測の平均値を採用した場合、正規分布を仮定すると1観測が標準偏差内に落ちる確率は68.3%です。t分布では自由度1ですから、標準偏差内に落ちる確率はt分布表から50%にすぎないことがわかります。すなわち、少ない観測値に対して標本分布として正規分布を仮定した場合、計画機関は品質の悪い成果を受け入れる可能性があります。逆に、作業機関である測量業者にとっては、成果検定が緩やかになる可能性があります。なお、公共測量作業規程の準則において、測量成果の品質管理にt分布は使われていません。
参考文献
1.蓑谷千凰彦(1995):推定と検定のはなし、東京図書.
2.中根勝見(2018):日本における誤差論の歴史的考察、写真とリモートセンシング Vol.57.No4、152-159. または、アイサンテクノロジー株式会社 Website
https://atmsp.aisantec.com/atmspark/modules/IA_34/index.php?id=12
3.Ramachandran, K.M. & Tsokos, C.P.: Mathematical Statistics with Applications (2009), Elsevier Academic Press.
パラメータ情報
【地殻変動補正提供サービス】パラメータの生成と評価:2019年12月1日~12月31日
2019年11月29日
2019年12月1日から2019年12月31日を有効期間とする
地殻変動補正提供サービス パラメータを生成しましたので、お知らせいたします。
パラメータの精度評価結果は以下の通りです。
水平方向の推定誤差の平均値は、0.012 mです。
水平方向の推定誤差の標準偏差は、0.041 mです。
水平方向の推定誤差が4cm以下の地域の割合は、99.23%です。
なお、今回生成したパラメータは、すべての電子基準点のデータを使用し、
パラメータの生成および精度評価を行っています。
今後、パラメータと評価指標の精度向上のため、
解析条件を変更する可能性がありますので、予めご了承ください。