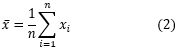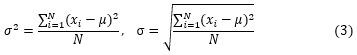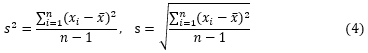2. 統計学の導入

統計学は、ばらつき（誤差）のあるデータから数学の手法でデータの性質や意味を見出す学問です。

私達も測定データを処理して目的とする情報(位置や高さなど)を適切に得るには統計学の助けを借りることになります。

 

2.1 母集団とサンプリング（標本抽出）

ある一つの量の測定を同一方法・条件で繰りかえし行うとその平均（系統誤差はないとして）は真の値に近づくと考えられます。

 

そこで、仮想的に無限回の繰り返しで得られる値の集まりを母集団(注3)と呼びます。母集団を知ることが観測の目的ですが、私たちは有限回の測定値しか手元にないため真の値は推定するしかありません。

 

統計学の言葉でいえば、母集団からの有限個のランダム（偏りのない）な標本値の抽出(サンプリング)によって、母集団のパラメータ(例えば平均値や分散など)の推定値を求めるということになります。統計学の用語では、母集団を特徴づけるパラメータを母数、その推定値を統計量といいます。

 

多数の測定をして得られた測定値は、すべてが同じではなく値には変動があります。そのため、平均だけではなく各測定値が平均からどのくらい変動しうるかも調べなければなりません。

 

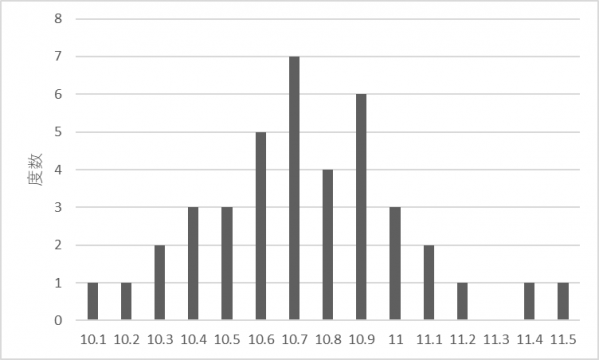
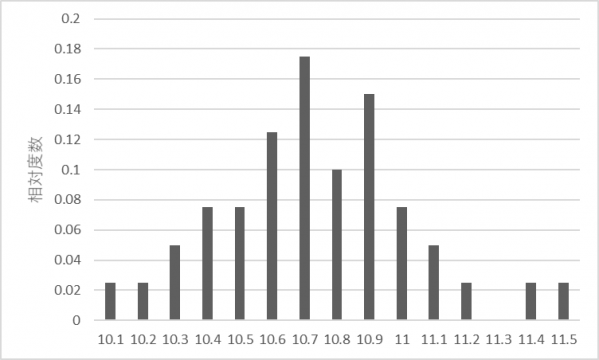
度数分布は測定値がどのように分布しているかを表したもので、変数(測定値)がある値をとる頻度を与えます(図2上)。度数を正規化して相対度数にすると、変数がある値をとる割合を示します(図2下)。

 

私たちが最終的に知りたいのはnを無限大にした分布ですが、これは後で述べる数学的に抽象化された確率分布につながっています。

 

図2．度数分布と相対度数分布（サンプル数：n=40）

 

• (注3)　母集団の要素の数を大きさと呼びますが、母集団の大きさは無限の場合と有限の場合があります。工業製品の抜き取り検査などでは有限ですが、ここで取り扱っているような同一条件での繰り返し測定や国民全体を対象とした調査などでは無限あるいはほとんど無限に近くなります。

 

2.2 基本的な概念

統計学で使われる基本的な概念について紹介しましょう。

 

平均(算術平均)

一つの量を繰り返しn回測定したとき、平均値は以下のとおりです。

 

中央値

n個の測定値を大きさの順に並べたときの中央の値のこと。

 

とすると、nが奇数なら中央値はですが、偶数の時はとします。

 

分散、標準偏差

平均値からのずれの2乗の平均が分散、その正値の平方根が標準偏差で測定値のばらつきを表します。

母集団の平均値が既知なら母集団の大きさをN（Nが無限ならNとする）として、

は、母集団分散と呼ばれます。

 

分散（標準偏差）には実はもう一つの式があります。

 

ここでnはサンプル数で、(3)式のNより当然小さくなります。

この式は、母集団のパラメータ推定という問題にかかわっています。母集団の値を推定するにはサンプリングを繰り返してその平均をとればよいと考えられます。

そのとき平均値の推定値は(1)と同じ式になりますが、標準偏差（分散）の推定値は(4)のようにnではなくn-1で割る式になります。ちなみに、式(4)のは、標本分散と呼ばれています。

 

参考文献

Meyer, S. L. : Data Analysis for Scientists and Engineers, John Wiley & Sons, 1992.

中川徹・小柳義夫: 最小二乗法による実験データ解析: 東京大学出版会, 1987.

東京大学教養学部統計学教室編: 自然科学の統計学, 東京大学出版会, 2016.

 

 

第2回は確率と確率分布についてです。