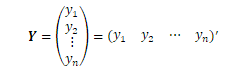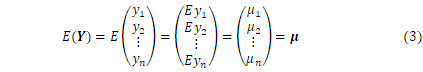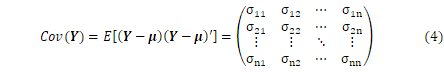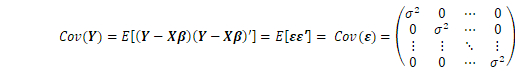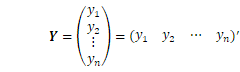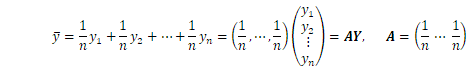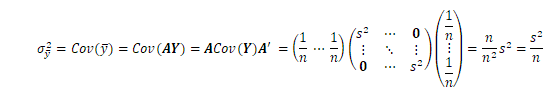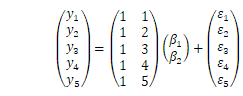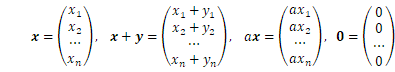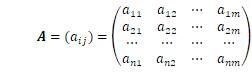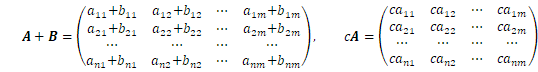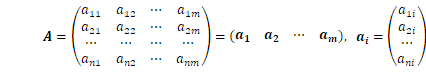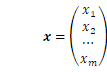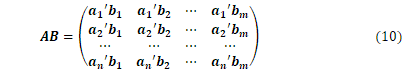今回から、線形モデルとその解法に入ります。線形モデルは前回も紹介したようにデータ(の期待値)とパラメータの関係が線形であるようなモデルです。例えば、P、Qの座標をそれぞれとし点PQ間のGNSS基線ベクトルをと表せば、となり観測値との座標の関係は１次（線形）関係で表せます。実は測量では多くの場合（辺長や角観測と座標の関係など）、モデルは線形ではありませんが線形になるように近似して解いています。非線形モデルの線形近似については後の回でお話しします。

 

線形モデルの記述にはベクトルや行列を用いるのが便利ですので、それらを取り扱う線形代数の基礎的な事柄を付録にまとめておきました。必要に応じて参照していただければと思います。

 

1.線形モデルの表現

個の測定データのベクトルを、

 

 

個の未知パラメータからなるベクトルを

 

 

ランダム誤差のベクトルを

 

 

としたとき、線形モデルは次のように表されます。

 

 

は行列で計画(モデル)行列と呼ばれ、各成分は既知の定数です。

また、

 

 

を仮定しておきます。はと同じです。は確率変数で観測値は誤差を含みますが、その期待値がパラメータの線形式で表せるということです。

 

上式では期待値、は共分散をとることを示します。期待値や分散の定義については第2、4回で紹介していますが、複数個の変数がある場合、ベクトル及び行列で表現すると取り扱いが便利です。具体的に書くと、以下のようになります。

 

確率変数ベクトルの期待値は

 

 

確率変数間の分散を成分に持つ共分散行列(誤差行列)が次のように定義されます。

 

 

線型モデルでは、

 

です。

 

また、とをそれぞれ定数行列及びベクトルとした時、の線形変換に関して次の式が成り立ちます。

 

 

2番目の式は誤差伝播則と呼ばれています。確率変数を変換したとき、その誤差は元の変数の誤差で表せる（誤差が伝わってゆく）という意味です。

 

誤差伝播の例：

①観測値の和と差

 

2つの独立な観測値との和（差）

 

の分散はとのの分散をそれぞれととすると、 なので(6)から

 

 

標準偏差は、となります。

 

②観測値の定数倍

 

       なら

 

です。

 

③平均値の誤差

ある量(例えば基線長)を回観測したとします。すると平均値と(標本)分散は、

 

 

です（第１回参照）。平均値の誤差（分散）を求めてみましょう。観測値ベクトルは

 

 

です。平均値の式は

 

 

と書けますからの線形式です。従って、平均値の分散は(6)より

 

 

となり、１観測の分散のになります。また、標準偏差は平方根をとるのでになります（①と②を応用してはをからまで足したものと考えれば、分散は=と求まります。）。

 

これから線形モデルを用いてパラメータの推定や検定を行うわけですが,今回は(2)の条件の他に計画行列はフルランクと仮定しておきます（2．でわかるように正規方程式が逆行列で解ける場合です）。そうでない場合（ランク落ちという）は、後の回で取り上げます。一つだけ例をあげれば、GNSSによる基線ベクトル観測から位置を求める場合、最低１点の３次元座標を固定することにより、正規方程式の逆行列が存在します。固定点がないとランク落ちとなり逆行列では解けません。

 

2.　パラメータ推定法とその性質１：最小二乗法

2.1　線形モデルの幾何学

線形モデルを幾何学的に考えてみましょう。観測ベクトルは、次元空間(データ空間)内のある点を示します。は計画行列を

 

 

と列ベクトルに分けると

 

 

と書けます。各列ベクトルは次元ですからデータ空間内にあり、の列ベクトルが張る空間(：推定空間といいます)はデータ空間の部分空間となっています。そしてはの値に応じた推定空間内の点を表しています。それと観測値のベクトルとの差が誤差ベクトルとなります。問題は、もも未知ということです。しかし、はデータですから既知、また、は推定空間内にあります。

 

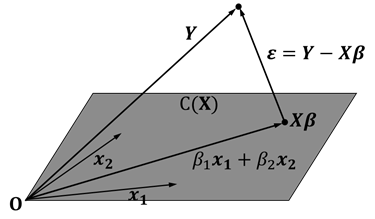
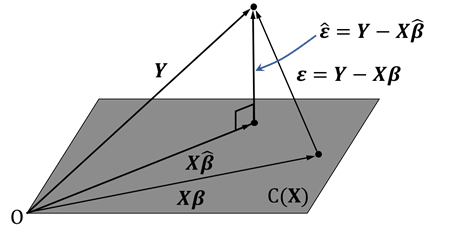
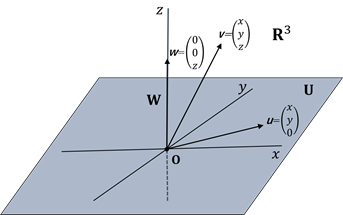
以上のことを3次元（）でイメージできるように図1で示しました。データは3次元空間内にあり、はとで張られる3次元空間内の平面でその中にがあります。

 

 

図1．線形モデルの幾何学

 

最小二乗の条件：推定値が

 

 

を満たすとき最小二乗解といいます(は最小値を示します)。

 

これは、との距離が最小になるということです。そして、そのようなベクトルは、残差が推定空間と直交するものとして与えられることがわかります(図2)。式で書くと残差のベクトルは計画行列の列ベクトルと直交するので(付録、(4))、

 

 

となります。従って、

 

 

つまり次式が成り立ちます。

 

 

これを正規方程式といいます。

 

がフルランクとするとのランクはとなって逆行列が存在します。従って正規方程式を解いて

 

 

が、最小二乗解となります。

 

および誤差の推定値は

 

 

 

となり、観測値は以下のように分解できます。

 

 

は直交射影と呼ばれるもので、今の場合をへ垂直に投影したもの(正射影)を与えます。は、次のような性質を持っています。

 

 

また、への正射影はただ一つに決まることが証明されます。従って最小二乗解も一意に決定されます。

 

図2．最小二乗法の幾何学

 

古い最小二乗法の教科書では、正規分布から最小二乗条件を導き出し、観測値Yを正規分布に従うと仮定していました。しかし、図2に示すように、最小二乗解は幾何学的に導かれ、観測値の正規分布の仮定は必要ありません。

 

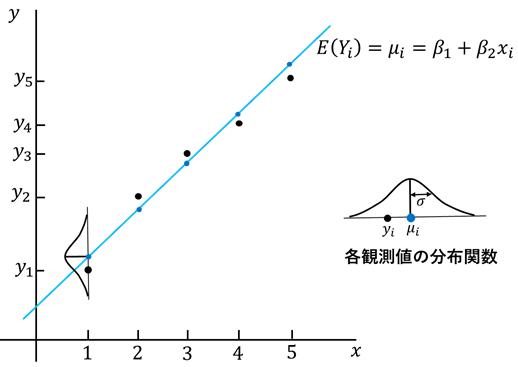
簡単な例として、前回紹介した直線回帰の問題を見てみましょう(図３)。

モデルとして、

 

 

各誤差の平均は、分散は

を考えます。ベクトルと行列で表現すると、

 

 

となります。は正則ですから逆を持ち、の最小二乗解が、

 

 

と求まります。

 

図３．簡単な直線回帰

 

 

2.2　最小二乗解の性質

最小二乗解は重要な性質をもっていますので、以下に述べたいと思います。まず、

最小二乗解の不偏性です。

最小二乗解の期待値をとると

 

となり不偏(期待値が真値に等しい)であることわかります。

 

最小二乗解の分散

最小二乗解は観測ベクトルの線形関数として与えられますから、誤差伝播により分散を持ちます。分散行列は、

 

     (6)より

 

となります。

 

ここで、は、未知量の重み係数行列と呼ばれ、未知量の精度に関係しています。正方行列のi番目の対角要素は、i番目の未知数の標準偏差で表されます。例えば、GNSS測位で観測点の位置をローカル座標系で表した場合、は4行４列で、緯度(n)、経度(e)、高さ(u)及び時間(t)が要素になっています。この要素からHDOP(水平DOP)が導かれます。

 

最良不偏推定値BLUE

推定値を求める時の基準としてBLUEというものがあります。BLUEとは(Best Linear Unbiased Estimator)の頭文字で最小の分散を持つ不偏な線形の推定値という意味です。これに関しては有名な次の定理があります。

 

ガウス‐マルコフの定理

 

推定可能とは、の線形式からなるの不偏推定量が存在するということです。今回の仮定では自体が最小二乗解として不偏ですからは推定可能です。がフルランクでない場合はの適当な一次式が推定可能となります。証明はここでは省略しますが、一般の教科書に載っていますので(例えば、参考文献2)興味ある方は参照してください。

 

2.3　誤差分散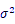の推定

残差の二乗和を考えましょう。モデルに最小二乗解を代入すると残差は、

 

 

となります。ここで、

 

ですから、残差は誤差ベクトルのみに依存することがわかります。そこで残差二乗和の期待値をとると、

 

 

となることがわかっています(参考文献2等参照)。従って、は残差二乗和から

 

 

と推定できることになります。を自由度といいます。はがフルランクなら未知パラメータの数と同じです。

 

次回は、一般の最小二乗法について紹介し、測量における線形モデルの簡単な例とその解についてお話ししたいと思います。

 

『第7回付録 線形(線型)代数の基礎』へ

 

『第8回 線形モデル – その2』へ

 

参考文献

1．Christensen, R.: Plane Answers to Complex Questions: The Theory of Linear Models (2011), Springer Texts in Statistics, New York.

2．東京大学教養学部統計学教室編: 自然科学の統計学（2016）, 東京大学出版会.

 

 

ベクトル、行列、ベクトル空間とその線型変換に関する数学の分野が線形(線型)代数ですが、統計学や最小二乗法で必要となる基本的なことをまとめておきます。

 

A0．集合及び演算の記号

集合に関して以下のような記号を使います。集合とはある定義されたものの集まりで、集合を構成するものを元といいます。

 

。

      

 

 また、

 

 

A1．ベクトル、ベクトル空間、行列

ベクトルは二次元や三次元空間の位置ベクトルなどでおなじみでしょう。ここでは、まずベクトル空間の定義をします。

 

ベクトル空間：集合があってその任意の元とスカラーに関して和とスカラー倍が定義されて、以下のような法則が成り立つときをベクトル空間といい、の元をベクトルといいます。（スカラーとはベクトルではない普通の数のことです）

 

 

つまり、ベクトルとは和とスカラー倍が定義され、和と積の（普通の）法則がみたされているものと考えられます。ベクトル空間のことを線形（線型）空間ともいいます。

また、ベクトルは太字（ボールド体）で書くことにします。

 

ベクトルは抽象的な概念ですが、私たちが取り扱うのはほとんど の場合で、スカラーも実数です。その時は、をn次元数ベクトル空間と考え、以下のように各ベクトルをn個の実数を縦に並べた列ベクトルとして書きます。

 

 

縦ベクトルと同じように横ベクトルも定義されます。横ベクトルは、「’」をつけて

 

 

となります。

 

部分（ベクトル）空間：の部分集合がそれ自体ベクトル空間の時、を部分（ベクトル）空間といいます。言い換えると、に含まれる元がまたベクトルとして和とスカラー倍の法則を満たすということです。

 

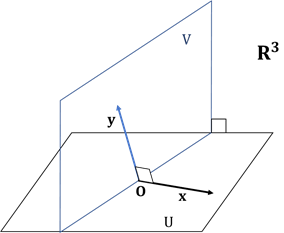
部分空間の例

3次元数ベクトル空間は、ですが、

 

は、その部分空間で平面となります。また、は、軸でこれも部分空間です。

は2次元の、は1次元のベクトル空間です（図A 1）。

 

図A1.　部分空間の例（）

 

 

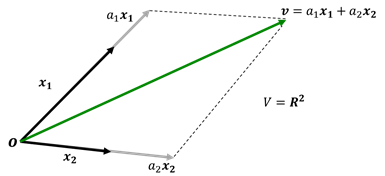
線形（一次）結合：いくつかのベクトルから和とスカラー倍で生じるベクトルを一次（線形）結合といいます。

 

 

ベクトルの一次結合全体からなる部分空間をで張られる空間といいます。

 

一次独立と一次従属：が成り立つのが、がすべて0である場合、は一次独立といい、そうでないとき一次従属といいます（図A2）。

 

基底：一次独立なが張る空間をとするとき、をの基底といいます。

ある空間の基底となるベクトルの数は一定です。

 

部分空間のランク：部分空間の基底の元の数を、その部分空間のランクといい、と書きます（図A3）

 

図A2.において、あるいはは一次独立、は一次従属.

 

図A3．は基底で張られ、ランクは2．

 

 

ベクトルの内積、直交、長さ、距離：においてはベクトルの内積が定義されます。

 

のとき、

 

ここで、は横ベクトルです。「’」 は転置といって縦と横を逆にすることを示す記号です（行列の項参照）。

 

の内積が0 ( の場合、は直交します。        (4)

 

2つの部分空間が直交するとは、ならとなることです(図A4)。

 

ベクトルの長さは、

 

 

の距離とは、差のベクトルの長さです。           (6)

 

図A4．直交部分空間の例：

 

行列：行列は数あるいは変数（要素）を長方形に並べたものです。また、ベクトルと同じようにここで取り扱う各行列要素はほとんどの場合実数です。行列は大文字のボールド体で書くことにします。

 

 

の縦（列）横（行）の長さを明記する時は、n行m列の行列、または行列といいます。

同じ型の行列には和とスカラー倍が定義され、

 

のとき、

 

 

ベクトルと同じ法則(1)を満たします。

 

 

など。

 

従って行列全体もベクトル空間を構成していることになります。

 

の列数との行数が等しい時に積が定義されます。のとき、型で、とすると

 

 

です。行列の積はスカラー倍とは違って、結果が掛ける順序に依存します。一般に

 

 

であることに注意してください。

次元縦ベクトルは、横ベクトルは行列と考えられます。ベクトルの内積(3)は、ベクトルとベクトルの積です。

 

行列の列空間：行列 の各列は、のベクトルです。

 

,

 

行列の列ベクトルが張る空間を列空間といいと書きます。

 

 

と書けますが、をm次元ベクトル

 

 

とすれば、

 

 

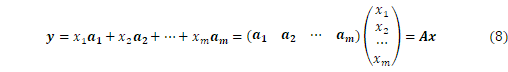
です。のランクを行列のランクといい、あるいはと書きます。ランクは空間を張る一次独立なベクトル(基底)の数でしたから、は一次独立な列ベクトルの数となります。実は一次独立な行ベクトルの数も同じです。

 

がならば、はフルランクといいます。ランクは一次独立な列(行)の数ですから、この場合可能な最大値をとります。また、

 

 

が成り立ちます。

 

行列を行ベクトル、列ベクトルに分けて以下のように書くと、

 

 

 

つまり、積の要素は内積となります。

 

行列の種類：いくつか定義をあげます。

正方行列：列と行の数が等しい行列。

 

転置行列：行と列を入れ替えた行列で、の転置行列をと書くと、です。また、です。

 

対称行列：なら対称行列といいます。対称行列は正方行列です。

 

対角行列：正方行列で対角成分以外が0の行列を対角行列といいます。です。特に、対角成分がすべて1の対角行列を単位行列といいと書きます。

 

単位行列は、積における１(単位元)で、が成り立ちます。ただし、がなら最初のは、つぎのはです。

 

逆行列：正方行列に対し、となる行列がある時、は正則であるといいをの逆行列といいます。行列が正則となる必要十分条件は、つまりの列がの基底となることです。

また、が正則ならも正則で、逆行列は

 

 

とが同じ大きさの正則行列ならも正則で、逆行列は

 

 

です。

 

その他の重要な行列の演算については後の回にまわすことにします。

 

『第8回 線形モデル – その2』へ

 

参考文献

線形代数に関してはたくさんの教科書が出ています。例えば、

1．佐竹一郎: 線型代数学(2000), 裳華房.

2．有馬哲: 線型代数入門(1975), 東京図書.

 

2020年3月1日から2020年3月31日を有効期間とする

地殻変動補正提供サービス パラメータを生成しましたので、お知らせいたします。

 

パラメータの精度評価結果は以下の通りです。

水平方向の推定誤差の平均値は、0.012 mです。

水平方向の推定誤差の標準偏差は、0.046 mです。

水平方向の推定誤差が4cm以下の地域の割合は、99.20％です。

 

なお、今回生成したパラメータは、すべての電子基準点のデータを使用し、

パラメータの生成および精度評価を行っています。

今後、パラメータと評価指標の精度向上のため、

解析条件を変更する可能性がありますので、予めご了承ください。