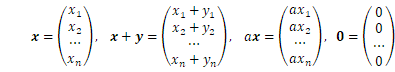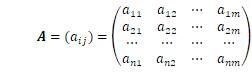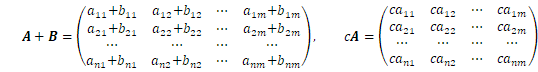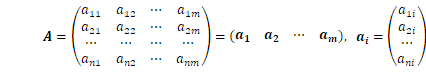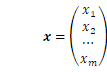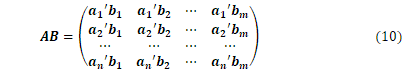誤差論と最小二乗法
第7回付録 線形(線型)代数の基礎
2020年02月13日
ベクトル、行列、ベクトル空間とその線型変換に関する数学の分野が線形(線型)代数ですが、統計学や最小二乗法で必要となる基本的なことをまとめておきます。
A0.集合及び演算の記号
集合に関して以下のような記号を使います。集合とはある定義されたものの集まりで、集合を構成するものを元といいます。
また、
A1.ベクトル、ベクトル空間、行列
ベクトルは二次元や三次元空間の位置ベクトルなどでおなじみでしょう。ここでは、まずベクトル空間の定義をします。
ベクトル空間:集合![]() があってその任意の元
があってその任意の元![]() とスカラー
とスカラー![]() に関して和とスカラー倍が定義されて、以下のような法則が成り立つとき
に関して和とスカラー倍が定義されて、以下のような法則が成り立つとき![]() をベクトル空間といい、
をベクトル空間といい、![]() の元をベクトルといいます。(スカラーとはベクトルではない普通の数のことです)
の元をベクトルといいます。(スカラーとはベクトルではない普通の数のことです)
つまり、ベクトルとは和とスカラー倍が定義され、和と積の(普通の)法則がみたされているものと考えられます。ベクトル空間のことを線形(線型)空間ともいいます。
また、ベクトルは太字(ボールド体)で書くことにします。
ベクトルは抽象的な概念ですが、私たちが取り扱うのはほとんど ![]() の場合で、スカラーも実数です。その時は、
の場合で、スカラーも実数です。その時は、![]() をn次元数ベクトル空間と考え、以下のように各ベクトルをn個の実数を縦に並べた列ベクトルとして書きます。
をn次元数ベクトル空間と考え、以下のように各ベクトルをn個の実数を縦に並べた列ベクトルとして書きます。
縦ベクトルと同じように横ベクトルも定義されます。横ベクトルは、「’」をつけて
となります。
部分(ベクトル)空間:![]() の部分集合
の部分集合![]() がそれ自体ベクトル空間の時、
がそれ自体ベクトル空間の時、![]() を部分(ベクトル)空間といいます。言い換えると、
を部分(ベクトル)空間といいます。言い換えると、![]() に含まれる元がまたベクトルとして和とスカラー倍の法則を満たすということです。
に含まれる元がまたベクトルとして和とスカラー倍の法則を満たすということです。
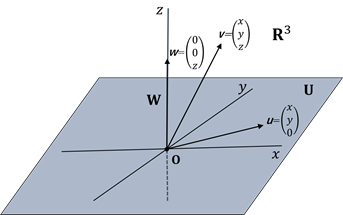
部分空間の例
![]() は、その部分空間で
は、その部分空間で![]() 平面となります。また、
平面となります。また、![]() は、
は、![]() 軸でこれも部分空間です。
軸でこれも部分空間です。
線形(一次)結合:いくつかのベクトルから和とスカラー倍で生じるベクトルを一次(線形)結合といいます。
ベクトル![]() の一次結合全体からなる部分空間を
の一次結合全体からなる部分空間を![]() で張られる空間といいます。
で張られる空間といいます。
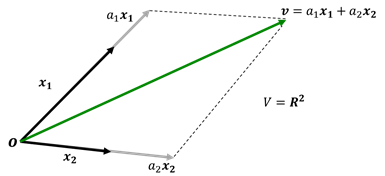
一次独立と一次従属:![]() が成り立つのが、
が成り立つのが、![]() がすべて0である場合、
がすべて0である場合、![]() は一次独立といい、そうでないとき一次従属といいます(図A2)。
は一次独立といい、そうでないとき一次従属といいます(図A2)。
基底:一次独立な![]() が張る空間を
が張る空間を![]() とするとき、
とするとき、![]() を
を![]() の基底といいます。
の基底といいます。
ある空間の基底となるベクトルの数は一定です。
部分空間のランク:部分空間![]() の基底の元の数を、その部分空間
の基底の元の数を、その部分空間![]() のランクといい、
のランクといい、![]() と書きます(図A3)
と書きます(図A3)
ベクトルの内積、直交、長さ、距離:![]() においてはベクトルの内積が定義されます。
においてはベクトルの内積が定義されます。
ここで、![]() は横ベクトルです。「’」 は転置といって縦と横を逆にすることを示す記号です(行列の項参照)。
は横ベクトルです。「’」 は転置といって縦と横を逆にすることを示す記号です(行列の項参照)。
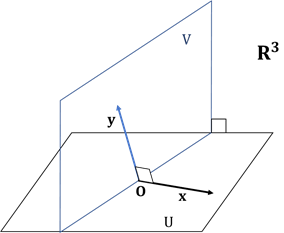
2つの部分空間![]() が直交するとは、
が直交するとは、![]() なら
なら![]() となることです(図A4)。
となることです(図A4)。
行列:行列は数あるいは変数(要素)を長方形に並べたものです。また、ベクトルと同じようにここで取り扱う各行列要素はほとんどの場合実数です。行列は大文字のボールド体で書くことにします。
![]() の縦(列)横(行)の長さを明記する時は、n行m列の行列、または
の縦(列)横(行)の長さを明記する時は、n行m列の行列、または![]() 行列といいます。
行列といいます。
同じ型の行列には和とスカラー倍が定義され、
ベクトルと同じ法則(1)を満たします。
![]() の列数と
の列数と![]() の行数が等しい時に積
の行数が等しい時に積![]() が定義されます。
が定義されます。![]() のとき、
のとき、![]() 型で、
型で、![]() とすると
とすると
です。行列の積はスカラー倍とは違って、結果が掛ける順序に依存します。一般に
であることに注意してください。
![]() 次元縦ベクトルは
次元縦ベクトルは![]() 、横ベクトルは
、横ベクトルは![]() 行列と考えられます。ベクトルの内積(3)は、
行列と考えられます。ベクトルの内積(3)は、![]() ベクトルと
ベクトルと![]() ベクトルの積です。
ベクトルの積です。
とすれば、
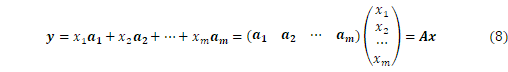
です。![]() のランクを行列
のランクを行列![]() のランクといい、
のランクといい、![]() あるいは
あるいは![]() と書きます。ランクは空間を張る一次独立なベクトル(基底)の数でしたから、
と書きます。ランクは空間を張る一次独立なベクトル(基底)の数でしたから、![]() は一次独立な列ベクトルの数となります。実は一次独立な行ベクトルの数も同じです。
は一次独立な列ベクトルの数となります。実は一次独立な行ベクトルの数も同じです。
![]() が
が![]() ならば、
ならば、![]() はフルランクといいます。ランクは一次独立な列(行)の数ですから、この場合可能な最大値をとります。また、
はフルランクといいます。ランクは一次独立な列(行)の数ですから、この場合可能な最大値をとります。また、
が成り立ちます。
行列の種類:いくつか定義をあげます。
正方行列:列と行の数が等しい行列。
転置行列:行と列を入れ替えた行列で、![]() の転置行列を
の転置行列を![]() と書くと、
と書くと、![]() です。また、
です。また、![]() です。
です。
対角行列:正方行列で対角成分以外が0の行列を対角行列といいます。![]() です。特に、対角成分がすべて1の対角行列を単位行列といい
です。特に、対角成分がすべて1の対角行列を単位行列といい![]() と書きます。
と書きます。
単位行列は、積における1(単位元)で、![]() が成り立ちます。ただし、
が成り立ちます。ただし、![]() が
が![]() なら最初の
なら最初の![]() は
は![]() 、つぎの
、つぎの![]() は
は![]() です。
です。
逆行列:正方行列![]() に対し、
に対し、![]() となる行列
となる行列![]() がある時、
がある時、![]() は正則であるといい
は正則であるといい![]() を
を![]() の逆行列といいます。
の逆行列といいます。![]() 行列
行列![]() が正則となる必要十分条件は
が正則となる必要十分条件は![]() 、つまり
、つまり![]() の列が
の列が![]() の基底となることです。
の基底となることです。
です。
その他の重要な行列の演算については後の回にまわすことにします。
『第8回 線形モデル – その2』へ
参考文献
線形代数に関してはたくさんの教科書が出ています。例えば、
1.佐竹一郎: 線型代数学(2000), 裳華房.
2.有馬哲: 線型代数入門(1975), 東京図書.