空間データの品質向上
第2回 交差の自動修正(2)
2012年08月22日
交差エラーとは
1.交差をしてはならないとしているが
公共測量作業規程の準則は、5条の3項で「計画機関は、得ようとする測量成果の種類、内容、構造、品質等を示す仕様書(以下「製品仕様書」という。)を定めなければならない。」と規定している。しかし、筆者が調査し以前に報告した内容(空間データの品質の第4回)では、ほとんどの計画機関が製品仕様書を作成していないと回答している。
準則は、品質を公共測量標準図式の45条、線の連続性で次のように規定している。
| (1) | 連続するデータは、座標一致で連続しなければならない。 |
| (2) | 真幅道路等は街区面が構成できるように、袋小路や施設入り口等の表現上、開放部においても当該取得分類に間断区分を設定して取得するものとする。 |
| (3) | 河川等において道路橋等の下を通過する箇所は、間断区分を設定して取得するものとする。但し、出入り口の調査が困難な用水路等はこの限りではない。 |
| (4) | 線の中間に別の線データが接する場合には、別の線データの端点座標は、接する線の線上になければならない。 |
また、46~48条には射影のある非対称記号、面データの特例、座標の方向について記載がある。このように交差に該当する部分は、(4)の線の中間に別の線データが接する場合には、別の線データの端点座標が接する線の線上になければならないとしている。ところが、この線上になければならないということが、ほとんどの確率で不可能である。
交差とは次のように定義することができる。
面オブジェクトは、その周辺境界を表現するのに、端点のみで2直線分が接続する閉じた連結線分群で、また、線オブジェクトは、端点のみで2直線分が接続する連結直線分群で表現し、それらの線分群をチェインとする、また、オブジェクトは,分岐やドーナツ状になっている内側の穴(ホール)の表現等で複数の連結直線分群で構成したものを1つのオブジェクトにするマルチパートも含む。
面オブジェクトのチェインが、閉じた連結直線分群で構成しているとすると、面オブジェクトと面オブジェクトの交差とは、それぞれのチェインが共通点を持ち、面オブジェクトAのチェインを構成する線分の端点(以下,チェインの端点)が、面オブジェクトBのチェインの内部にある場合をいう。また、面オブジェクトと線オブジェクトの交差とは、線オブジェクトのチェインが面オブジェクトのチェインと共通点を持ち、線オブジェクトのチェインの端点が面オブジェクトのチェインの内部にある場合をいう。そして、線オブジェクトと線オブジェクトの交差とは、それぞれのチェインの端点以外で共通点を持つ場合をいう。
そこで、航空写真測量における入力単位と描画端点とファイル上のチェインの端点の関係について説明することとする。
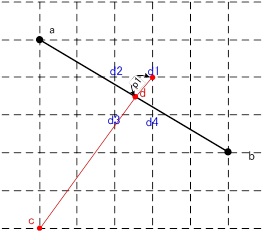
図1は、チェインabの線上にチェインcdのd点を一致させる場合の課題を例示したものである。図の破線で示されたグリッドは、入力単位を示している。作業規程の準則では、入力単位の最小値が1cm又は1mmと規定している。
図1で、チェインabの途中の線上にチェインcdを描画しようと場合、チェインabの線上のd点が入力単位のグリッド上にないため、結果的にファイル上のチェインの端点の座標はグリッド上の座標でしか記録されないので、d1~d4のいずれかの端点座標が記録される。ここで、チェインabとチェインcdの交点からd1またはd2をはみ出しとし、その幅または長さをはみ出し幅p1と表現することとする。
チェインabとチェインcdの交差をなくすためには、d点が必ずグリッド上の座標であることが必要であるが、作業規程では交差する双方のチェインに交点d点を挿入することを規定していないので、はみ出しとはみ出し幅p1が存在する。従って、チェインの途中で接続する場合で、数学的にチェインabとチェインcdに交点が存在し、p1がp1=(√2)/2以内のはみ出し幅のある場合の修正は、不可能と考えなければならない。
なぜなら、この概念は交差の修正を行う場合に大変重要で、入力単位×(√2)/2 以下の場合を修正しようとしても、解が見つからず無限ループに落ち込むからである。
論理一貫性の位相一貫性の交差の判定がプログラムで判定することが一般的である。しかし、多くの品質検査ツールは、はみ出し幅0mmで判定している。
筆者がある自治体の全域のDMデータを調査した交差の誤率は次の通りであった。
表1
| 対応 | 総要素数 | エラー数 | 誤率 |
| はみ出し幅0mmをエラーとして検査した場合 | 350,257 | 216,567 | 61.8% |
| はみ出し幅が10mm以上をエラーとした場合 | 350,257 | 780 | 0.2% |
このデータを見ても、修正不可能な入力単位以下の交差がいかに大半を占めていることがわかる。
筆者は、例え数学的に交差があるとしても、修正不可能な交差は、作業規程が間違っているのであって、エラーとはみなさないという見解である。また、品質検査ツールがはみ出し幅を0mmとして判定を行った場合は、入力単位以下の交差をエラーとしているが、目視によってOKエラーとしている。目視の時間(製造者にとって時間はお金である)と、その目視判断の結果が品質に重大な影響(合格のものを不合格とし、不合格のものを合格とする)を及ぼすこととなる。最初からOKエラーとするならば、品質検査ツールにその機能を持たすべきであると考えている。
市場に出回っている品質検査ツールの点検と、エラーの定義の見直しを行う必要があると考えている。また、筆者は交差のエラーを”はみ出し区間におけるはみ出し幅が入力単位×(√2)/2 以上の場合をエラーと定義する”ことを主張するものである。
2.交差パターン
交差の種類を表2で示すように分類することができる。
表2 空間属性と交差の関係
| 空間属性 | 線と線 | |||||
| 交差回数 | 1回交差(奇数交差) | 2回交差(偶数交差) | ||||
| 交差辺 | 同一辺 | 同一辺 | 異辺 | |||
| 交点後端点数 | 1点 | n点 | 1点 | n点 | 1点 | n点 |
| 空間属性 | 面と線 | |||||
| 交差回数 | 1回交差(奇数交差) | 2回交差(偶数交差) | ||||
| 交差辺 | 同一辺 | 同一辺 | 異辺 | |||
| 交点後端点数 | 1点 | n点 | 1点 | n点 | 1点 | n点 |
| 空間属性 | 面と面 | |||||
| 交差回数 | 1回交差(奇数交差) | 2回交差(偶数交差) | ||||
| 交差辺 | 存在しない | 同一辺 | 異辺 | |||
| 交点後端点数 | 存在しない | 存在しない | 1点 | n点 | 1点 | n点 |
交差には、空間属性が線と線、線と面、面と面の交差がある。
交差の特徴を述べるには、最初のチェインの端点が交差しているか否かが重要で、面と面面と線の場合は領域判定によって交差の状況を判定できる。しかし、線と線の場合は交差がわからない。そこで、ここでは、線と線の交差では、最初のチェインの端点が交差していないと仮定した場合について述べる。
| (1) | 交点回数は、奇数回と偶数回がある。 |
| (2) | 交点が1回の場合は、交点以降のチェインが交差している状態にある。 |
| (3) | 交点が2回以上の交点が偶数回数の場合は、奇数交点から次の交点(偶数交点)までが交差している状態で、最後の偶数交点から最後の端点までが交差していない状態である。 |
| (4) | 交点が2回以上の交点の奇数回数の場合は、奇数交点から次の交点(偶数交点)までが交差している状態で、最後の奇数交点から最後の端点までが交差していない状態である。 |
交差後のチェインの端点数に着目すると、次の特徴がある。
| (1) | 交差後チェインの端点が1点の場合と、数回存在するn点の場合がある。 |
| (2) | 交差は、交点が相手側の同じ辺に交点がある場合と、異なる辺に交点がある場合がある。 |
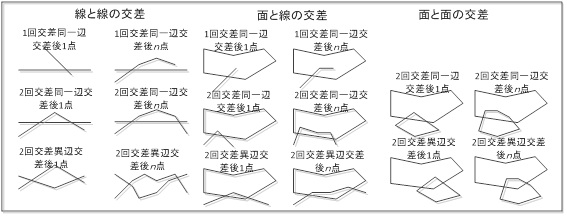
これらの代表的な交差パターンを図2に示す。
3.はみ出しとはみ出し幅
はみ出しとはみ出し幅とは次のように定義する。
はみ出しとは、面オブジェクトAと面オブジェクトBが交差している場合、面オブジェクトAのチェインが面オブジェクトBの内部にあるチェインを、面オブジェクトAが面オブジェクトBにはみ出したチェインと呼ぶこととする。同様に、面オブジェクトBのチェインが面オブジェクトAの内部にあるチェインを、面オブジェクトBが面オブジェクトAにはみ出したチェインと呼ぶこととする。また、面オブジェクトと線オブジェクトが交差している場合、線オブジェクトのチェインが面オブジェクトの内部にあるチェインを、線オブジェクトが面オブジェクトにはみ出したチェインと呼ぶこととする。
線オブジェクトA,Bが交差している場合,交差を境に交点の前後のいずれがはみ出しているかを特定できない。しかし、筆者が線交差のエラーを分析したところでは、オブジェクトのデータを入力する際に最初に入力した点をチェインの最初の端点とすると、最初の端点は、はみ出している例はほとんどなく、それ以外の端点でのはみ出しが圧倒的に多いことが分かった。そこでここでは、線オブジェクトA,Bのチェインの関係において、線オブジェクトA,Bのチェインの最初の端点が交差していないと仮定し、線オブジェクトAのチェインが線オブジェクトBの奇数交点から偶数交点までのチェインが線オブジェクトAにはみ出したチェインと呼ぶこととする。同様に線オブジェクトBのチェインが線オブジェクトAの奇数交点から偶数交点までのチェインが線オブジェクトBにはみ出したチェインと呼ぶこととする。また、はみ出し幅とは、はみ出しにおける一方のチェインの交差後の端点から他方の線分に下ろした垂線の足までの距離のうちで、一番長いものとする。
例えば、これを図で示すと、図3は、交差のはみ出しとはみ出し幅を示したものである。直線Aと直線Bは●が始点で、矢印がチェインの方向を示し、それぞれの始点ははみ出してしていないものとする。はみ出しの区間は、交点1から交点2までと、交点3から交点4までの区間で、交点1~2区間のはみ出し幅は一番長いp、交点3~4区間のはみ出し幅は一番長いqとする。
これからシリーズで述べる交差の自動修正ツールの交差の定義は、この考え方を前提としているのでぜひ、記憶にとどめておいていただきたい。