交差パターンと修正方法

1.線交差

オブジェクトの空間属性が線と線の交差および線と面の交差を線交差と呼ぶこととする。線交差を修正することを考えて6種類のパターンに分類した。

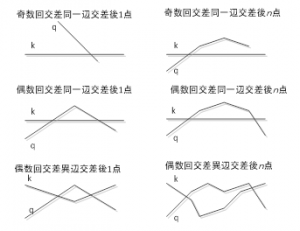
図1 線交差のパターン

ここで、オブジェクトのチェインは、座標列の2点を結ぶ線分の連結線分と定義しているので、すべての座標点を端点と表現する。

交差は、交差の回数と、交差後のチェインの端点数によって表現できる。交差の回数は、前回も述べたように、チェインの始点が交差していないとすると次のことが言える。

(1)	交点が1点の場合は、交点以降のチェインの終点までがはみ出していることを示している。
(2)	交点が複数の場合、交点1から交点2の区間がはみ出しいる状態にあり、交点2から交点3の区間がはみ出していない状態にある。
(3)	交点が2点以上の偶数交点の場合は、奇数交点から偶数交点の間がはみ出していて、偶数交点から奇数交点までがはみ出していないことを示している。
(4)	交点が2点以上の奇数交点の場合は、奇数交点から偶数交点の間がはみ出していて、偶数交点から奇数交点の間がはみ出していなく、なおかつ、最後の奇数交点から以降のチェインの終点までがはみ出していることを示している。

修正の原則は、はみ出し区間の交差するオブジェクト間に優位差がある場合と同順位の場合に、はみ出し区間のはみ出し幅が閾値以内（描画誤差程度の現地寸法40~50cm程度を想定）の場合に修正を行う。
図2は、線分kと線分qの関係で優位差がある場合の線分kが優位とした場合と、同順位の場合を示す。また、図2の赤線は修正した線分を示している。

図2 交差と修正

注）図2の修正するはみ出し幅は、理解しやすいように実際に修正するはみ出し幅より強調して描いてあります。

1回交差同一辺交差後の端点が1点の場合は、交差する地物の優位差に関係なく、交点以降をカットする。
1回交差同一辺交差後の端点がn点の場合で優位差がある場合は、交差後オブジェクトqのみ出し区間のチェインをオブジェクトkのチェインの線上に移動させる。優位差がない場合には、双方のオブジェクトをはみ出し幅の半分を反対方向に移動させはみ出しを解消させる。
以下、2回交差同一辺交差後1点、2回交差同一辺交差後端点n点、2回交差異辺交差後1点、2回交差異辺交差後n点も上記と同様に、優位差がある場合は、交差後オブジェクトqのみ出し区間のチェインをオブジェクトkのチェインの線上に移動させ、優位差がない場合には、双方のオブジェクトをはみ出し幅の半分を反対方向に移動させはみ出しを解消させる。
また、面と線の交差の場合は、オブジェクトkを面とすると、原則的に面が優先するのでオブジェクトqの交差後のチェインをオブジェクトkのチェインの線上に移動させる。

2.面交差

オブジェクトが異なる場合の面と面の交差で優位差がある場合の修正は、交差後の優位差の低いオブジェクトのチェインのはみ出し区間を、優先順位の高いオブジェクトのチェインの線上に移動させる。
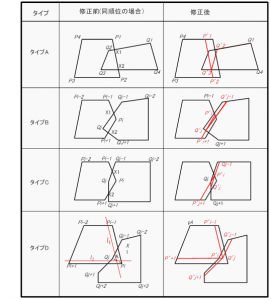
オブジェクトが同種の場合の面と面の交差の修正は、同順位の交差となる。修正は、図3のように行なう。
タイプAは、交差が同一辺にある。このタイプは同一辺の交点がX1,X2の2点で交差し、交差後の端点が1点以上である。
点Q₂,Q₃それぞれから線分P₁P₂に垂線を下ろし、どちらか長い距離の半分の距離分だけ線分P₁P₂を平行移動させ、線分P’₁P’₂を求める。線分P’₁P’₂と線分Q₂Q₃の交点を求め、交点から線分Q₂Q₃に向かって垂線を下ろし、その距離を求める。求めた距離分だけ線分Q₂Q₃を平行移動させ線分Q’₂Q’₃を求める。修正後の形状は、オブジェクトPがP’₁,P’₂,P₃P₄、オブジェクトQがQ’₁,Q₂,Q’₃Q₄となる。
タイプBは、交点が異なる辺にあり交差後の端点が1点で2つのチェインの交点を結ぶ線分X₁X₂に端点P_i,Q_jが異なる側にあるものをいう。
チェインのはみ出し部分で構成する端点[X₁,P_i,X₂,Q_j]のうち対角となる2点を線分で結び、この線分と選択されなかった2点からの離れ距離をd(A⊥BC)として表現すると、この組合せは以下の4通りがある。

a₁=d(P_i⊥Q_jX₂)　a₂=d(X₁⊥Q_jX₂) ･･･①

b₁=d(Q_j⊥P_iX₂)　b₂=d(X₁⊥P_iX₂) ･･･②

c₁=d(P_i⊥Q_jX₁)　c₂=d(X₂⊥Q_jX₁) ･･･③

d₁=d(Q_j⊥P_iX₁)　d₂=d(X₂⊥P_iX₁) ･･･④

上記①～④組合せのうち、それぞれ長い方の距離を選択する。

a_max=a₁ (a₁>a₂)　or　a_max=a₂ (a₁<a₂)

b_max=b₁ (b₁>b₂)　or　b_max=b₂ (b₁<b₂)

c_max=c₁ (c₁>c₂)　or　c_max=c₂ (c₁<c₂)

d_max=d₁ (d₁>d₂)　or　d_max=d₂ (d₁<d₂)

選択した線分の構成点が同じ端点(P_iまたはQ_j)をもつもの同士で組み合わせる。
各組み合わせの2つの距離のうち、短いものを選択し，その距離の1/2を修正移動距離とする。

t_p=b_max/2　(b_max<d_max) or　･･･⑤

t_p=d_max/2　(b_max>d_max) 　　･･･⑥

t_q=a_max/2　(a_max<c_max) or　･･･⑦

t_q=c_max/2　(a_max>c_max) 　　･･･⑧

選択した短い距離の対辺となる線分を垂直方向に上記で求めた距離分を平行移動させる。
タイプ Bのうち、2点を結ぶ線分の長さをd(A,B)と表現すると、次の条件を満たすものをタイプCとする。

d(X₁,P_i)<d(P_i,X₂) & d(Q_j,X₁)<d(X₂,Q_j)

または

d(X₁,P_i)>d(P_i,X₂) & d(Q_j,X₁)>d(X₂,Q_j)

この場合の修正方法はタイプBと同じであるが、計算式⑤～⑧の移動距離がタイプBではb_max,d_max,a_max,c_maxの距離の1/2であるのに対して、タイプCは1であるところが異なる。
交点が異なる辺にあり交差後の端点が1点で、2つのチェインの交点を結ぶ線分X₁X₂に対して端点P_i,Q_jが同じ側にある場合をタイプDとする。
チェインの端点のうち、互いのチェインとはみ出しの端点を結んだ線分P_iQ_jの中点を求め点Aとし、チェイン1の線分P_i-1P_iをその傾きを保ったまま点Aを通るように平行移動させた線分をl₁とする。同様に線分P_iP_i+1をその傾きを保ったまま点Aを通るように平行移動させた線分をl₂とする。線分P_i-2P_i-1と線分l₁の交点をP’_i-1とし、線分P_iP_i+1と線分l₂の交点をP’_i+1とし、線分l₁と線分l₂の交点をP’_iとする。また、チェイン2も同様に処理し，修正を行う。

図3 面と面の同順位の交差と修正

注）図3の修正するはみ出し幅は、理解しやすいように実際に修正するはみ出し幅より強調して描いてあります。

3.補正処理

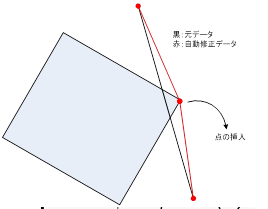
交差が図4のように面オブジェクトの線オブジェクトが面オブジェクトのコーナーを横切る場合、面オブジェクトを面オブジェクトの外周によって修正した場合に、線オブジェクトに微小線分の発生、直線性の喪失が発生する。そこでこのような場合には面オブジェクトの突起している端点を挿入することによって線オブジェクトの微小線分発生の防止と、直線性を維持している。

図4 コーナーを横切る場合の補正

このように、修正は、オブジェクトの空間属性、オブジェクト間の優位差、交点数、交差後の端点数、修正後の補正等を考慮して行う。

次回は、このアルゴリズムに基づいたツールを使って検証した、実証例について紹介することとする。