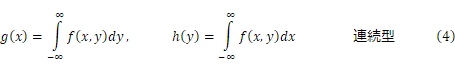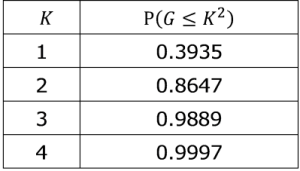誤差論と最小二乗法
第4回 その1 – 多次元の確率変数と確率分布
2019年10月07日
私たちが実際に取り扱う現象は、一つの確率変数で記述できるとは限りません。例えば、衛星測位の場合、3次元位置の場合は3つ、水平位置なら2つの変数になります。多次元の場合、相関や共分散など一次元ではなかった概念が出てきます。以下、簡単のため2つの確率変数の場合で説明したいと思います。一般の場合に拡張するのはそれほど難しくありません。
1.同時確率分布と周辺確率分布
2つの確率変数![]() を考えましょう。これらが同時に
を考えましょう。これらが同時に![]() となる確率:
となる確率:![]() を同時確率分布といいます。
を同時確率分布といいます。![]() は2変数の関数
は2変数の関数![]() :同時確率密度関数で表されます。
:同時確率密度関数で表されます。![]() は一次元の時と同様に確率分布の条件である、
は一次元の時と同様に確率分布の条件である、
![]()
を満たす必要があります。ここでSは![]() の取り得る範囲(一般に2次元平面)です。
の取り得る範囲(一般に2次元平面)です。
周辺確率分布
![]() のうち一つだけに注目した時の確率分布を周辺確率分布といいます。密度関数は、
のうち一つだけに注目した時の確率分布を周辺確率分布といいます。密度関数は、
![]()
が得られ、これらを周辺確率密度関数といいます。例えば、![]() の離散同時確率分布
の離散同時確率分布![]() が表1のように与えられていたとしましょう(
が表1のように与えられていたとしましょう(![]() )。周辺確率分布は文字通り周辺にあり、
)。周辺確率分布は文字通り周辺にあり、![]() のようになります。さらにグラフ化したものが図1です。
のようになります。さらにグラフ化したものが図1です。
表1.同時確率分布と周辺確率分布の例
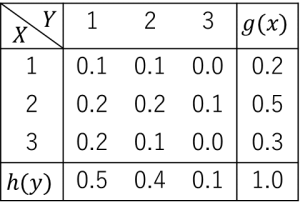

図1.表1のグラフ
条件付確率分布
条件付確率は第2回で出てきました。ある事象Bが起こった時に他の事象Aが起こる確率でした。そこでBを![]() 、Aを
、Aを![]() とすると、その確率は、
とすると、その確率は、
![]()
となります。これから![]() および
および![]() の条件付確率密度関数が周辺確率分布を使って、それぞれ次のように定義されます。
の条件付確率密度関数が周辺確率分布を使って、それぞれ次のように定義されます。
例えば、![]() は
は![]() が与えられた時の
が与えられた時の![]() の確率分布となります。上の例で
の確率分布となります。上の例で![]() として計算してみると、
として計算してみると、
となります。
周辺確率密度関数も条件付確率密度関数も確率分布としての条件(負にならないこと、すべての値における確率の和が1)を満足しています。
2.期待値、共分散、相関係数
確率変数の期待値は周辺確率分布から1変数と同様に計算できます。例えば、Xを連続型とすれば期待値及び分散は、
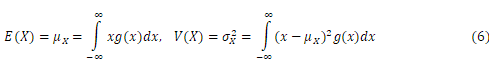
となります。
次にX+Yの分散を計算してみましょう。
となり、一般に
![]()
です。これは二つに変数の間に関連があるためです。そこで、次のように共分散と相関係数が定義されます。
共分散:
相関係数:
相関係数は、2変数が関連して変化する傾向の度合いを示します。共分散の定義式からわかるように、Xの小さい値がYの小さい値と関連し、Xの大きい値もYの大きい値に関連する傾向があれば共分散は正となり、相関係数も正です。逆に、Xの小さい(大きい)値とYの大きい(小さい)値が関連していると、共分散と相関係数は負となります。そのような関係が認められないと共分散と相関係数は0に近くなります(図2)。
2変数が独立〈次項参照〉の場合は定義から共分散は0になります。ただし、逆に共分散が0でも変数が独立とは限りません。共分散は確率的に平均的な傾向を示すものだからです。
(第4回 その2 多次元の確率変数と確率分布 につづく)
誤差論と最小二乗法
第4回 その2 – 多次元の確率変数と確率分布
3.独立な確率変数
二つの事象がお互いに影響を及ぼさない場合を互いに独立といって、二つが同時に起こる確率は各々の確率の積になることを第2回に紹介しました。同様に、確率変数が互いに独立とは、同時確率分布がそれぞれの周辺確率分布の積になることを言います。式で書けば、
です。この場合、期待値や分散は各変数のものを独立に求めればよいので、計算が簡単になります。独立な確率変数の和などに関する結果は、以下のとおりです。
期待値
分散
特にn個の確率変数が同じ確率分布(平均値:![]() 、分散:
、分散:![]() )に従うときは、
)に従うときは、
標準偏差は、
![]()
となります。
測量では、各観測値は独立であると考えて処理するのが一般的です。
4.2次元の正規分布
ここで、よく使われる確率分布として2次元の正規分布について紹介しておきましょう。導出は統計の教科書(例えば、第2回参考文献2)に譲るとして、![]() の同時確率密度関数は以下のような式になります。
の同時確率密度関数は以下のような式になります。
ここで、
です。
![]() は楕円の式ですから、等確率
は楕円の式ですから、等確率![]() を結んだ等高線は楕円となり(図3)、楕円内で確率密度関数を積分すると
を結んだ等高線は楕円となり(図3)、楕円内で確率密度関数を積分すると![]() の値が楕円内に入る確率となります。
の値が楕円内に入る確率となります。
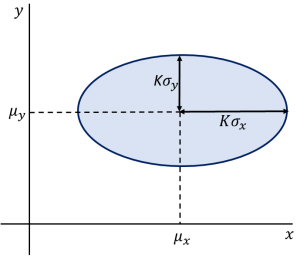
2次元正規分布は、衛星測位での水平位置の誤差や基準点測量で誤差楕円を求める時の基礎になっています(参考文献1、2)。
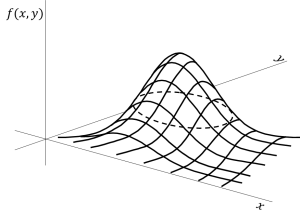
図3. 2次元正規分布
特に、2変数に相関がない場合![]() の2次元正規分布を考えましょう。この場合、(10)式から、
の2次元正規分布を考えましょう。この場合、(10)式から、
ですから同時確率分布は1次元正規分布の積になり、2変数は独立であることがわかります(これは正規分布だけの性質です)。この場合、等高線は、
となり、中心が![]() 、2軸の径が
、2軸の径が![]() 、
、![]() となる楕円です(図4)。
となる楕円です(図4)。![]() がその楕円内に入る確率
がその楕円内に入る確率![]() は、
は、
と計算されます(計算の詳細は略)。いくつかの![]() に対する確率を表2にあげておきます。
に対する確率を表2にあげておきます。
1次元の正規分布では、値が![]() に入る確率は約68%、
に入る確率は約68%、![]() に入る確率は約95%でした(第3回参照)。多次元になると標準偏差内に入る確率が違うことがわかります。測量では、特に
に入る確率は約95%でした(第3回参照)。多次元になると標準偏差内に入る確率が違うことがわかります。測量では、特に![]() の時に誤差を表す楕円を誤差楕円と呼んでいます。
の時に誤差を表す楕円を誤差楕円と呼んでいます。
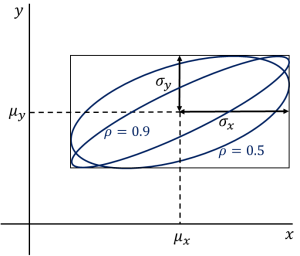
なお、![]() に相関がある一般の場合は、楕円は細くなり傾きます(図5)。
に相関がある一般の場合は、楕円は細くなり傾きます(図5)。
参考文献
1.センチメータ級測位補強サービスの利用とその品質の解説(2019)、アイサンテクノロジー株式会社 技術情報.(http://g-spatial.com/knowledge/tech_info/clas_use_and_quality/)
2.中根勝見、横井貴史(2015):衛星測位時代における測地学・ISO・測量法に基づく地球上の位置を表す理論とその仕組み、アイサンテクノロジー株式会社.
パラメータ情報
【地殻変動補正提供サービス】パラメータの生成と評価:2019年11月1日~11月30日
2019年10月31日
2019年11月1日から2019年11月30日を有効期間とする
地殻変動補正提供サービス パラメータを生成しましたので、お知らせいたします。
パラメータの精度評価結果は以下の通りです。
水平方向の推定誤差の平均値は、0.012 mです。
水平方向の推定誤差の標準偏差は、0.040 mです。
水平方向の推定誤差が4cm以下の地域の割合は、99.23%です。
なお、今回生成したパラメータは、すべての電子基準点のデータを使用し、
パラメータの生成および精度評価を行っています。
今後、パラメータと評価指標の精度向上のため、
解析条件を変更する可能性がありますので、予めご了承ください。