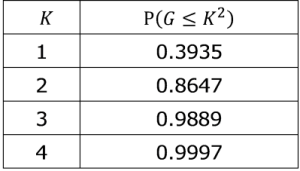誤差論と最小二乗法
第4回 その2 – 多次元の確率変数と確率分布
2019年10月07日
3.独立な確率変数
二つの事象がお互いに影響を及ぼさない場合を互いに独立といって、二つが同時に起こる確率は各々の確率の積になることを第2回に紹介しました。同様に、確率変数が互いに独立とは、同時確率分布がそれぞれの周辺確率分布の積になることを言います。式で書けば、
です。この場合、期待値や分散は各変数のものを独立に求めればよいので、計算が簡単になります。独立な確率変数の和などに関する結果は、以下のとおりです。
期待値
分散
特にn個の確率変数が同じ確率分布(平均値:![]() 、分散:
、分散:![]() )に従うときは、
)に従うときは、
標準偏差は、
![]()
となります。
測量では、各観測値は独立であると考えて処理するのが一般的です。
4.2次元の正規分布
ここで、よく使われる確率分布として2次元の正規分布について紹介しておきましょう。導出は統計の教科書(例えば、第2回参考文献2)に譲るとして、![]() の同時確率密度関数は以下のような式になります。
の同時確率密度関数は以下のような式になります。
ここで、
です。
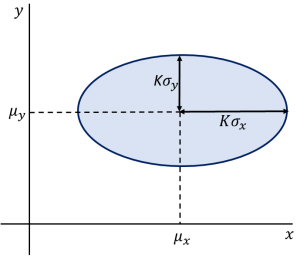
![]() は楕円の式ですから、等確率
は楕円の式ですから、等確率![]() を結んだ等高線は楕円となり(図3)、楕円内で確率密度関数を積分すると
を結んだ等高線は楕円となり(図3)、楕円内で確率密度関数を積分すると![]() の値が楕円内に入る確率となります。
の値が楕円内に入る確率となります。
2次元正規分布は、衛星測位での水平位置の誤差や基準点測量で誤差楕円を求める時の基礎になっています(参考文献1、2)。
図3. 2次元正規分布
特に、2変数に相関がない場合![]() の2次元正規分布を考えましょう。この場合、(10)式から、
の2次元正規分布を考えましょう。この場合、(10)式から、
ですから同時確率分布は1次元正規分布の積になり、2変数は独立であることがわかります(これは正規分布だけの性質です)。この場合、等高線は、
となり、中心が![]() 、2軸の径が
、2軸の径が![]() 、
、![]() となる楕円です(図4)。
となる楕円です(図4)。![]() がその楕円内に入る確率
がその楕円内に入る確率![]() は、
は、
と計算されます(計算の詳細は略)。いくつかの![]() に対する確率を表2にあげておきます。
に対する確率を表2にあげておきます。
1次元の正規分布では、値が![]() に入る確率は約68%、
に入る確率は約68%、![]() に入る確率は約95%でした(第3回参照)。多次元になると標準偏差内に入る確率が違うことがわかります。測量では、特に
に入る確率は約95%でした(第3回参照)。多次元になると標準偏差内に入る確率が違うことがわかります。測量では、特に![]() の時に誤差を表す楕円を誤差楕円と呼んでいます。
の時に誤差を表す楕円を誤差楕円と呼んでいます。
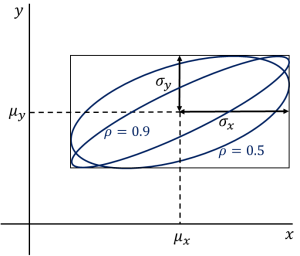
なお、![]() に相関がある一般の場合は、楕円は細くなり傾きます(図5)。
に相関がある一般の場合は、楕円は細くなり傾きます(図5)。
参考文献
1.センチメータ級測位補強サービスの利用とその品質の解説(2019)、アイサンテクノロジー株式会社 技術情報.(http://g-spatial.com/knowledge/tech_info/clas_use_and_quality/)
2.中根勝見、横井貴史(2015):衛星測位時代における測地学・ISO・測量法に基づく地球上の位置を表す理論とその仕組み、アイサンテクノロジー株式会社.