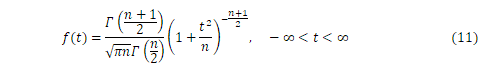ナレッジ
第5回 その2 – 統計的推論
2019年11月06日
3.正規分布からの標本
この項では特に母集団が正規分布からの標本分布を考えます。正規分布は第3回に述べたように統計学における基本の分布ですから、ここで導かれる統計量はさまざまな場面で活用される重要なものです。
正規分布は次の重要な性質をもっています。
(i)正規確率変数の線型変換は正規確率変数: ![]() が正規分布
が正規分布![]() に従うとき、
に従うとき、![]() は正規分布
は正規分布![]() に従う。
に従う。
(ii)独立な正規確率変数の和は正規確率変数:![]() を独立な確率変数とし、各
を独立な確率変数とし、各![]() は平均
は平均![]() 分散
分散![]() を持つ正規分布に従うとする。その時、
を持つ正規分布に従うとする。その時、![]() の分布は、平均
の分布は、平均![]() 、分散
、分散![]() の正規分布となる。
の正規分布となる。
つまり独立で正規分布に従う確率変数は、和や差をとったり定数倍しても再び正規分布となるのです。
例えば、測量において、距離、方向及び比高などあらゆる観測値を標準偏差で割った標準化変数![]() を使うことによって、こうした異種観測値が同時網平均できることになります。
を使うことによって、こうした異種観測値が同時網平均できることになります。
3.1 標本平均の分布-分散が既知の時
正規母集団の平均と分散をそれぞれ![]() 、
、![]() とすれば、標本平均は
とすれば、標本平均は![]() ですから(ii)を適用して(
ですから(ii)を適用して(![]() とすればよい)、
とすればよい)、
これは、一つのものを繰り返し観測した場合、推定値の精度を2倍にしたければ観測数は4倍にしなければならないことを示しています。
標本分散は、
ですから、その分布を知るためには確率変数の二乗和が従う分布が必要になります。正規分布に従う確率変数の二乗和の分布が![]() (カイ二乗)分布です。
(カイ二乗)分布です。
確率変数![]() が、
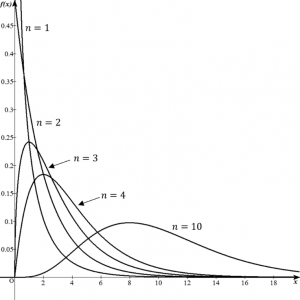
が、![]() を正の整数として次の形の確率密度関数を持つとき、自由度
を正の整数として次の形の確率密度関数を持つとき、自由度![]() の
の![]() (カイ二乗)分布
(カイ二乗)分布![]() といいます(図1)。
といいます(図1)。
ここで、![]() はガンマ関数という関数で、
はガンマ関数という関数で、![]() のとき、
のとき、![]() が成り立ち、
が成り立ち、![]() という値をとります。
という値をとります。
さて、![]() を正規母集団
を正規母集団![]() からのランダムサンプルとします。これを標準化して
からのランダムサンプルとします。これを標準化して![]() とすると各
とすると各![]() は標準正規分布の確率変数となります。この時、それらの二乗和
は標準正規分布の確率変数となります。この時、それらの二乗和
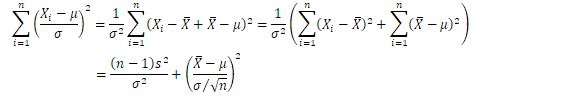
と変形すると、左辺は自由度![]() の
の![]() 分布、右辺第2項は自由度1の
分布、右辺第2項は自由度1の![]() 分布を持ちます。このことと(詳しい証明は省きますが)
分布を持ちます。このことと(詳しい証明は省きますが)![]() と
と![]() が独立なことから、右辺第1項が自由度
が独立なことから、右辺第1項が自由度![]() の
の![]() 分布に従うことがわかります。つまり、
分布に従うことがわかります。つまり、![]() を正規母集団からの標本分散としたとき統計量、
を正規母集団からの標本分散としたとき統計量、
は自由度![]() の
の![]() 分布に従います。これを使えば、標本分散から母分散について統計的推論を行うことが可能になります。また、後に述べる最小二乗法では残差の二乗和に対して
分布に従います。これを使えば、標本分散から母分散について統計的推論を行うことが可能になります。また、後に述べる最小二乗法では残差の二乗和に対して![]() 分布を用いて検定を行います。
分布を用いて検定を行います。
3.3 標本平均の分布-分散が未知の時:t分布
3.1で母集団の分散が既知ならば標本平均![]() の分布は正規となり、
の分布は正規となり、![]() は標準正規分布に従うことを見ましたが、一般的には母集団の分散は未知です。その場合、母分散の代わりに標本分散を使うことが考えられます。標本のサイズが大きい時は
は標準正規分布に従うことを見ましたが、一般的には母集団の分散は未知です。その場合、母分散の代わりに標本分散を使うことが考えられます。標本のサイズが大きい時は![]() と仮定でき中心極限定理により
と仮定でき中心極限定理により![]() が近似的に
が近似的に![]() に従うことがわかります。しかし、標本が小さい場合この仮定は使えず、
に従うことがわかります。しかし、標本が小さい場合この仮定は使えず、![]() は(スチューデントの)t分布というものになることが知られています。t分布は、小標本
は(スチューデントの)t分布というものになることが知られています。t分布は、小標本![]() の場合に有用な分布です。
の場合に有用な分布です。
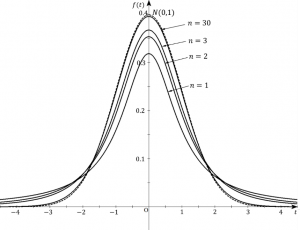
(スチューデントの)t分布
![]() と
と![]() が独立の確率変数で、
が独立の確率変数で、![]() が自由度
が自由度![]() の
の![]() 分布、
分布、![]() が
が![]() に従うとします。その時、確率変数、
に従うとします。その時、確率変数、
になります(図2)。t分布は左右対称なので平均は0、また、![]() なら分散は
なら分散は![]() です。
です。![]() が大きくなるとt分布は標準正規分布に収束することが証明されており、図2からもわかるように
が大きくなるとt分布は標準正規分布に収束することが証明されており、図2からもわかるように![]() が30以上では標準正規分布で近似しても問題ありません。
が30以上では標準正規分布で近似しても問題ありません。
正規母集団からのランダムサンプルの場合、次が成り立ちます。
大きさ![]() の標本平均と分散をそれぞれ
の標本平均と分散をそれぞれ![]() 、
、![]() 、母集団平均と分散をそれぞれ
、母集団平均と分散をそれぞれ![]() 、
、![]() とすると統計量、
とすると統計量、
なぜなら、
となって、![]() と
と![]() が独立なことから
が独立なことから![]() と
と![]() も独立になり、t分布
も独立になり、t分布![]() に従う統計量の定義(10)に合致するからです。
に従う統計量の定義(10)に合致するからです。
t分布は、正規分布の代用とも考えられますが、小標本の場合の厳密な確率分布です。図2を見ると正規分布はt分布よりピークがとがっています。そのため小標本の場合、正規分布を使うと平均からはずれる確率を過小評価していることになります。
例えば、2回の観測の平均値を採用した場合、正規分布を仮定すると1観測が標準偏差内に落ちる確率は68.3%です。t分布では自由度1ですから、標準偏差内に落ちる確率はt分布表から50%にすぎないことがわかります。すなわち、少ない観測値に対して標本分布として正規分布を仮定した場合、計画機関は品質の悪い成果を受け入れる可能性があります。逆に、作業機関である測量業者にとっては、成果検定が緩やかになる可能性があります。なお、公共測量作業規程の準則において、測量成果の品質管理にt分布は使われていません。
参考文献
1.蓑谷千凰彦(1995):推定と検定のはなし、東京図書.
2.中根勝見(2018):日本における誤差論の歴史的考察、写真とリモートセンシング Vol.57.No4、152-159. または、アイサンテクノロジー株式会社 Website
https://atmsp.aisantec.com/atmspark/modules/IA_34/index.php?id=12
3.Ramachandran, K.M. & Tsokos, C.P.: Mathematical Statistics with Applications (2009), Elsevier Academic Press.