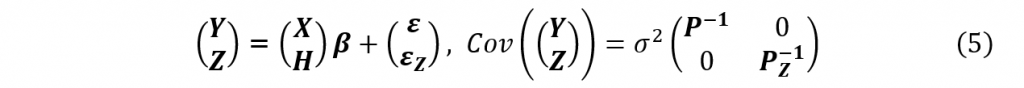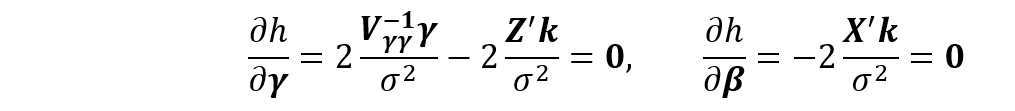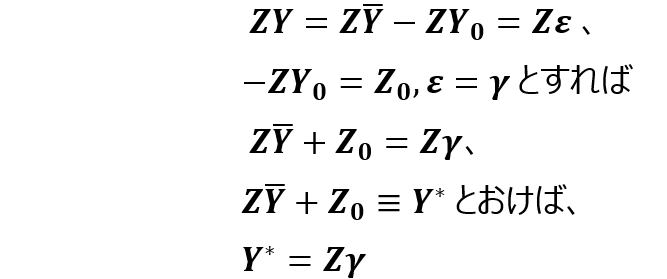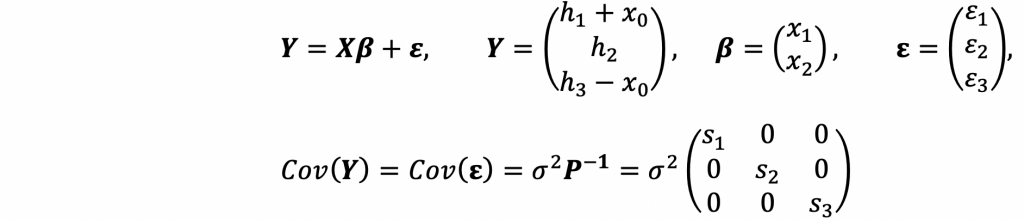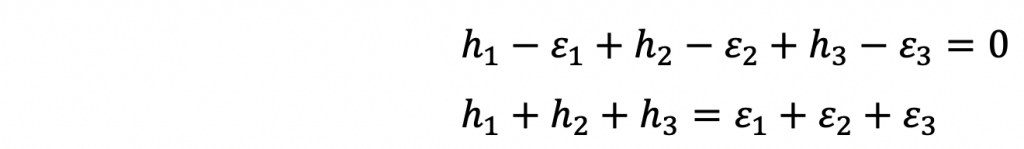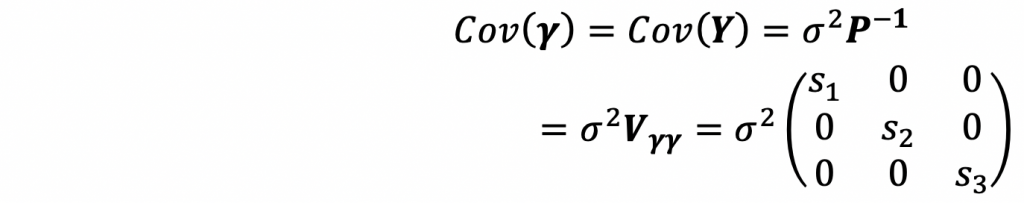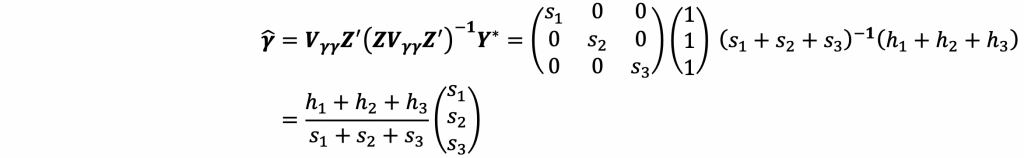誤差論と最小二乗法
第10回 様々な条件が付いた最小二乗法
2020年08月07日
実際に問題を解く場合には基本の線形モデルに条件を付加したり、先験的な情報を与える場合があります。例えば、観測値がある未知パラメータについてあまり敏感でないようなとき(パラメータが変化しても観測値がほとんど変化しない)、計画行列がランク落ちの状態に近くなり、正規方程式が解けないか、あるいは解けても解の誤差が非常に大きくなってしまいます。そのような場合は、パラメータを先験的に既知の値に拘束したり、新しい観測値を追加して正規方程式を解けるようにします。今回は、パラメータに拘束条件が付く場合と、混合モデルについて解説します。また、前回の内容も含めた具体例をいくつか紹介したいと思います。
1.観測の追加
パラメータが共通で別の観測方法で得られたデータがある場合、そのデータを追加することによって新しい情報を得られることがあります。もともとの観測方程式
にもう1セットの観測、
を加えれば、観測方程式は
となります。
ただし、モデルが異種の観測値に対し理論的に矛盾がないか、測定誤差の正しい見積もりにより重みが適切に表されているかなど注意する必要があります。測量でも、測地網平均において、距離観測、角観測、衛星観測などを統合して解析する場合があります。
2. パラメータに拘束条件があるモデル
未知パラメータの間に線形関係がある場合を考えます(線形でない場合は線形化しておきます)。
ここで、![]() は既知の
は既知の![]() 行列でランクは
行列でランクは![]() 、
、![]() は
は![]() 定数ベクトル、
定数ベクトル、![]() は拘束条件
は拘束条件![]() の重畳行列です。モデルは次のような形になります。
の重畳行列です。モデルは次のような形になります。
上の式を(3)と比べて見ると、![]() を仮想の追加観測値として取り扱えばよいことが分かります。その結果、正規方程式は、次のように元の式に新しい情報が追加された形となります。
を仮想の追加観測値として取り扱えばよいことが分かります。その結果、正規方程式は、次のように元の式に新しい情報が追加された形となります。
いくつかの代表的な場合を以下に示します(参考文献1参照)。
2.1 絶対値拘束条件
パラメータの値を初期値として先験的に与え、その値に拘束するものです;
この場合、先験的な初期値![]() を観測値として扱うことになります。網平均計算では、ある基準点の座標を(ある重みをつけて)先験値に拘束することに相当します。
を観測値として扱うことになります。網平均計算では、ある基準点の座標を(ある重みをつけて)先験値に拘束することに相当します。
2.2 相対値拘束条件
パラメータ間の関係を導入
一般には、
基準点の座標の場合、2点の相対位置を拘束することに相当します。
グローバルな宇宙測地観測による局位置と速度を求めるときに出てくるNNT(No-Net-Translation)
やNNR(No-Net-Rotation)などは拘束条件の例です。
拘束条件を強くしていくと、パラメータの値やパラメータ間の関係を完全に固定することになります。その場合、パラメータを消去して少ないパラメータの式を解いたり、ラグランジュの未定係数法(付録C3参照) を用いて正規方程式を解く方法があります。
3.混合モデル
標準の線形モデルにおいて、観測値の誤差![]() が未知パラメータの線形式で表されると仮定すると、混合モデルが得られます。式で書くと、
が未知パラメータの線形式で表されると仮定すると、混合モデルが得られます。式で書くと、
となります。ここで、![]() は未知パラメータですが確率変数です。元のモデルを書き換えると
は未知パラメータですが確率変数です。元のモデルを書き換えると
となります(![]() は
は![]() ベクトル、
ベクトル、![]() は既知の
は既知の![]() 行列、
行列、![]() は
は![]() 未知数ベクトル、
未知数ベクトル、![]() は
は![]() 未知誤差ベクトル確率変数)、
未知誤差ベクトル確率変数)、![]() は既知の
は既知の![]() 行列でランクは
行列でランクは![]() )。これが混合モデルの観測方程式です。
)。これが混合モデルの観測方程式です。
混合モデルは、観測値のベクトルがもともと他の観測値の線形結合、
の場合、と考えることができます。![]() を観測値
を観測値![]() の誤差クトルと考えると式(10)が得られます。
の誤差クトルと考えると式(10)が得られます。
を最小にすればよいのですが、![]() は完全に自由に動けず最終的な観測値
は完全に自由に動けず最終的な観測値![]() と未知変数
と未知変数![]() による
による![]() 個の条件
個の条件
を満たさなければなりません。そこで、ラグランジュの未定係数法を使います。ラグランジュ関数は、![]() を
を![]() ベクトルとして
ベクトルとして
より、
が得られます。左辺の行列は正則なので解くことができ(詳細略)、
そして、
となります。
条件方程式による解法
が得られます。
この時の解は
です。
もし、基本の線形モデルにおいて、![]() という関係があれば、モデルを条件方程式に変形させることができます。
という関係があれば、モデルを条件方程式に変形させることができます。
![]() において
において![]() (
(![]() の回りで
の回りで![]() を線形化したもの)と考えましょう。
を線形化したもの)と考えましょう。![]() をかけると、
をかけると、
(18)式には![]() ががありませんから、混合モデルの解法において式の数が
ががありませんから、混合モデルの解法において式の数が ![]() 個少なくなり、未知数は
個少なくなり、未知数は![]() 個となります。
個となります。![]() ならば、
ならば、
元のモデルより未知数が減り計算量が少なくてすみます。そのため、コンピュータ時代以前の測地網平均では、多くがこのような形にして解かれていました。
例題:水準測量
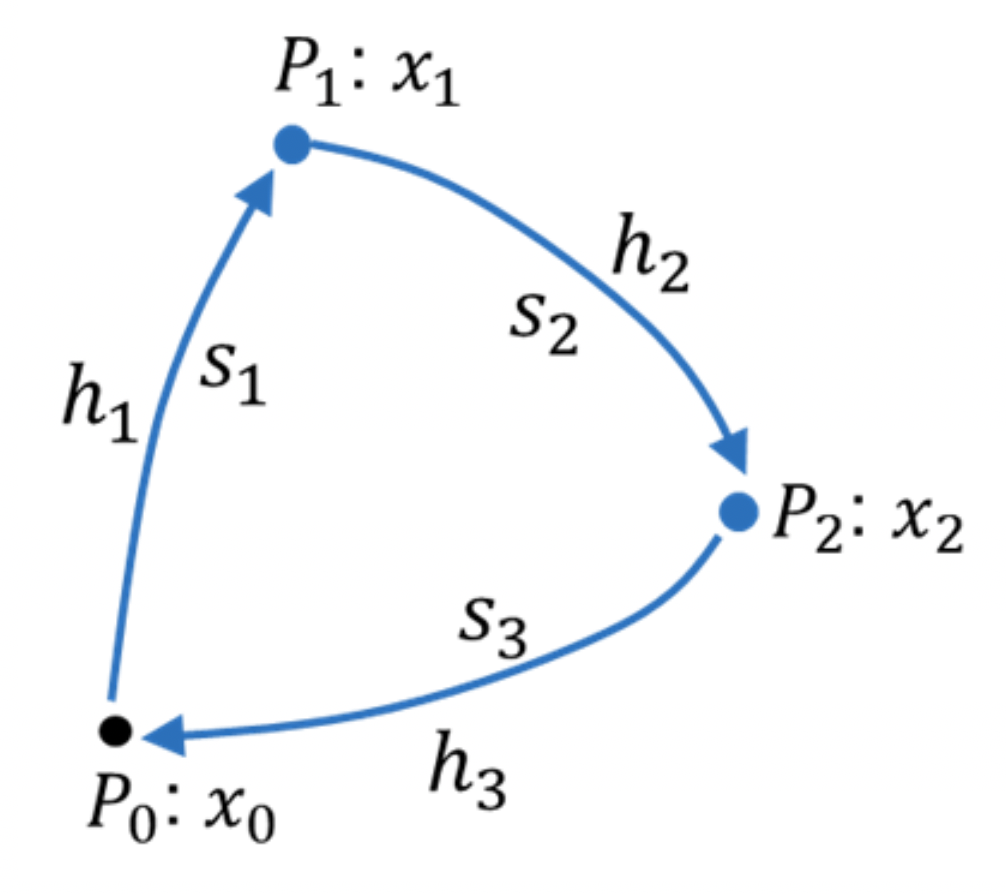
第8回の例1と同じ問題です(下図)。既知点![]() の標高が
の標高が![]() 、未知点
、未知点![]() の標高が道パラメータ
の標高が道パラメータ![]() 、測定値は比高
、測定値は比高![]() です。線形モデルは、
です。線形モデルは、
でした。
水準路線は一周していますから、標高差の総和(環閉合差)は0になるはずです。ただし誤差がありますから、
これを
として行列で書くと、
また、
となり、(11)の条件方程式の形となります。
解は(19)より、
従って、
となって、当然ですが一般の最小二乗解と同じになります。この場合、条件方程式は1つだけなので、最小二乗解法よりも未知数の数が減っています。
基準点網の平均計算でも、座標の閉合差や方向角の閉合差を考えると、条件方程式を立てることができます。
4.具体例の紹介
当社顧問中根勝見による資料(場所は?)を紹介しますので、参照してください。いくつか注意点を述べましょう。統計的仮説検定では、何を検定するかによって採用する統計量が異なります(第9回の付録も見てください)。
- 平均値の検定(資料の2.4)では、
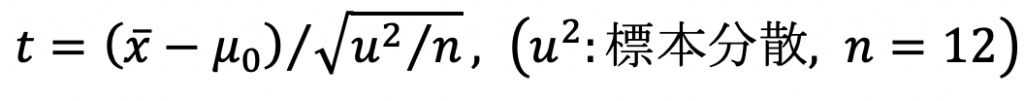 を計算して、
を計算して、 分布の限界値と比べています。
分布の限界値と比べています。 に対応する
に対応する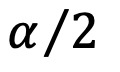 パーセント点は
パーセント点は (
( 分布表あるいはエクセルから)です。
分布表あるいはエクセルから)です。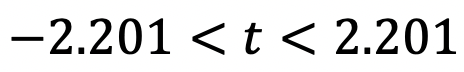 ならば、統計的にはスタティックの値と差がないということです。
ならば、統計的にはスタティックの値と差がないということです。 - 平均値の差の検定(2.5)は、9回では述べていませんが、2つの標本を統合した分散(式2.5) とそれに対応する
 検定量(2.6)を比べます。
検定量(2.6)を比べます。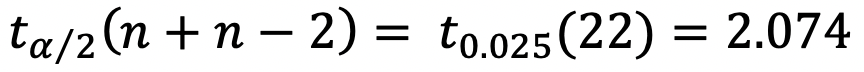 です。
です。 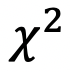 検定(資料の4)では最小二乗法による網平均結果の検定を行っています(第9回1.参照)。どのような条件を付けるかで5つの場合が示されています。既知点座標を固定せず、観測値として扱う方法は今回の2.1で述べました。採択の範囲は、
検定(資料の4)では最小二乗法による網平均結果の検定を行っています(第9回1.参照)。どのような条件を付けるかで5つの場合が示されています。既知点座標を固定せず、観測値として扱う方法は今回の2.1で述べました。採択の範囲は、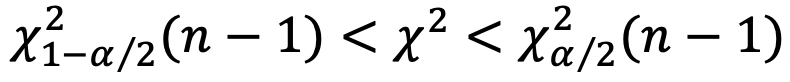 で、例えば、
で、例えば、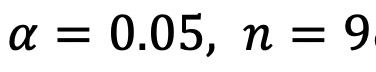 とすると、
とすると、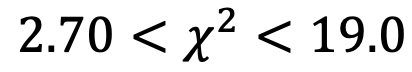 となります。 最小二乗法では
となります。 最小二乗法では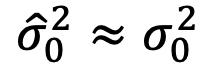 (ここでは1)、あるいは
(ここでは1)、あるいは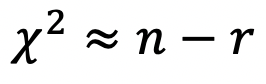 ( 自由度)ならば問題ないとみなせますが、この例のように適切な重量や固定点の選び方が大事ということが分かります。
( 自由度)ならば問題ないとみなせますが、この例のように適切な重量や固定点の選び方が大事ということが分かります。- 分散を比べるにはF分布を使います(資料の5)
 で、、母分散が等しい
で、、母分散が等しい と仮定すれば、
と仮定すれば、 となります。資料では分散の比を計算し、
となります。資料では分散の比を計算し、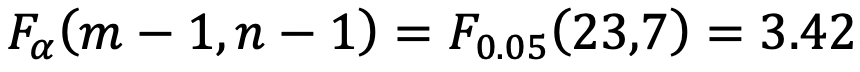 よりも小さければ採択(統計的に分散の差はない)です。
よりも小さければ採択(統計的に分散の差はない)です。
参考文献
- Dach, S. Lutz, P. Walser, P. Fridez, Bernese GNSS Software Version 5.2, Springer, University of Bern, Bern Open Publishing, 2015. http://www.bernese.unibe.ch
- Koch, K-R., Parameter Estimation and Hypothesis Testing in Linear Models, Springer, 1999.
- 中根勝見、統計的仮説検定の計算例