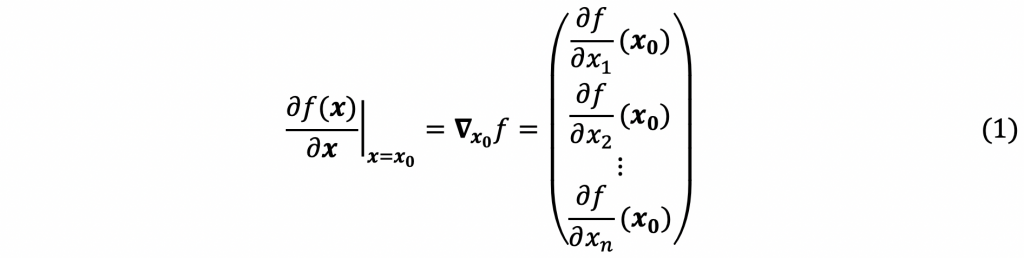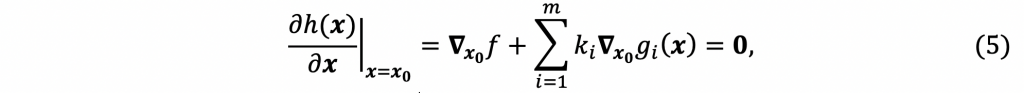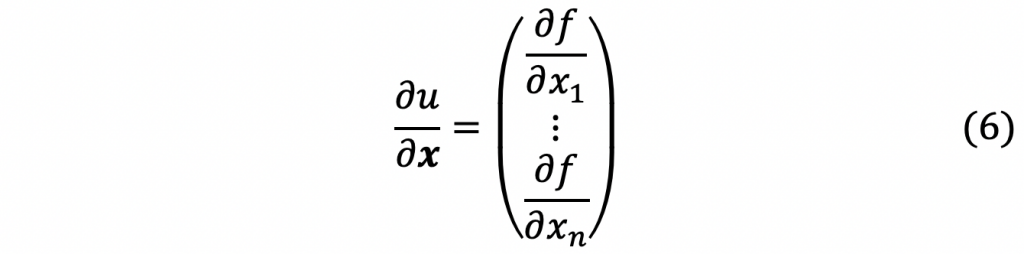C３. 関数の極大・極小とラグランジュの未定係数法

　関数がある点で極大値あるいは極小値（極値）をとるときは、そこで微分が0になります。ラグランジュの未定係数法は、拘束条件があるときに関数の極大・極小を求める問題です。

が、微分可能な実数値関数のとき、ベクトル

 

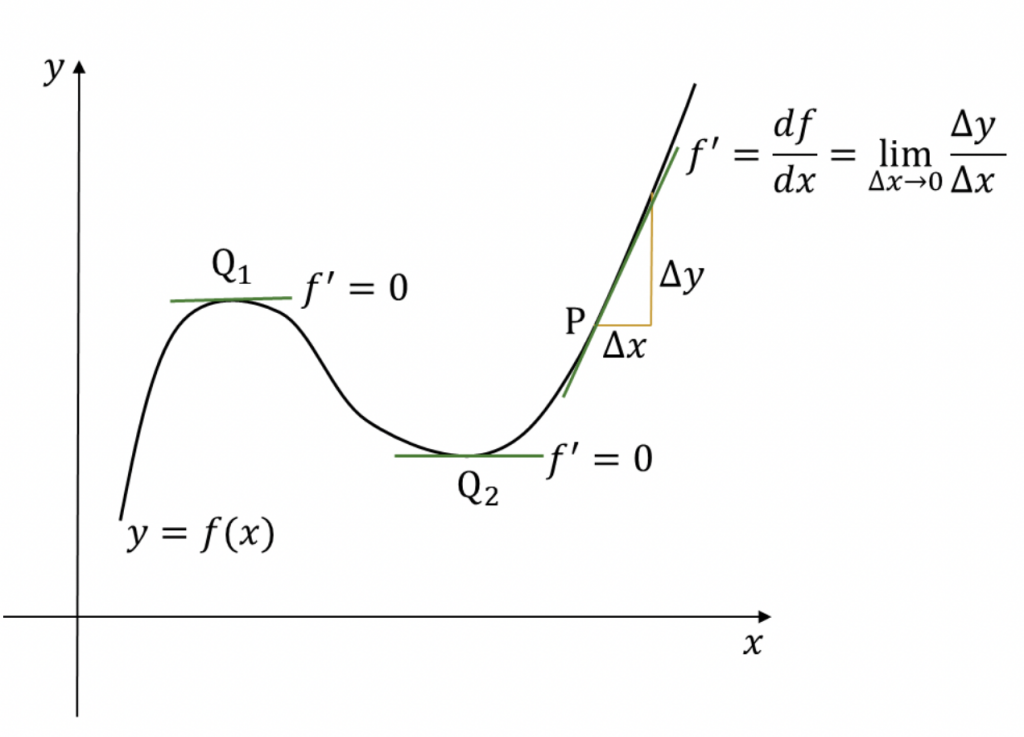
をのにおける勾配(gradient)ベクトルといいます。これは1変数の場合の微分係数を拡張したものです。1変数の関数が極値をとるとき微分係数が0となります（図1）。多変数の場合は以下の通りです。

図1．関数の極値：で、微分係数が0

 

関数の極値

を微分可能な実数値関数とし、で極値を持つとします。その時

となります。これは何の条件もない一般の場合ですが、もし、に何らかの拘束条件があるときの極値を求める問題がラグランジュの未定係数法です。

 

ラグランジュの未定係数法

が、拘束条件

の下、で極値を持つとします。ここで、各は微分可能で、勾配ベクトルは一次独立とします。

そのときベクトル（ラグランジュの未定係数）が存在して,ラグランジュ関数

がで極値を持ちます。つまり

 

となります。従って、式(5)を(3)とともに解けば、未知数であるとが求まります（図2）。

 

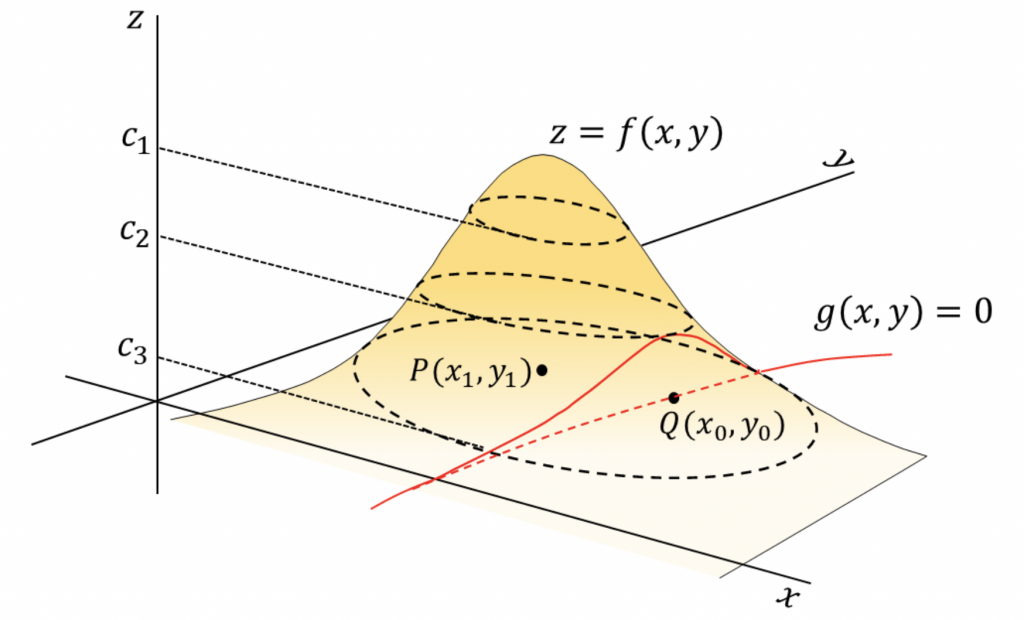
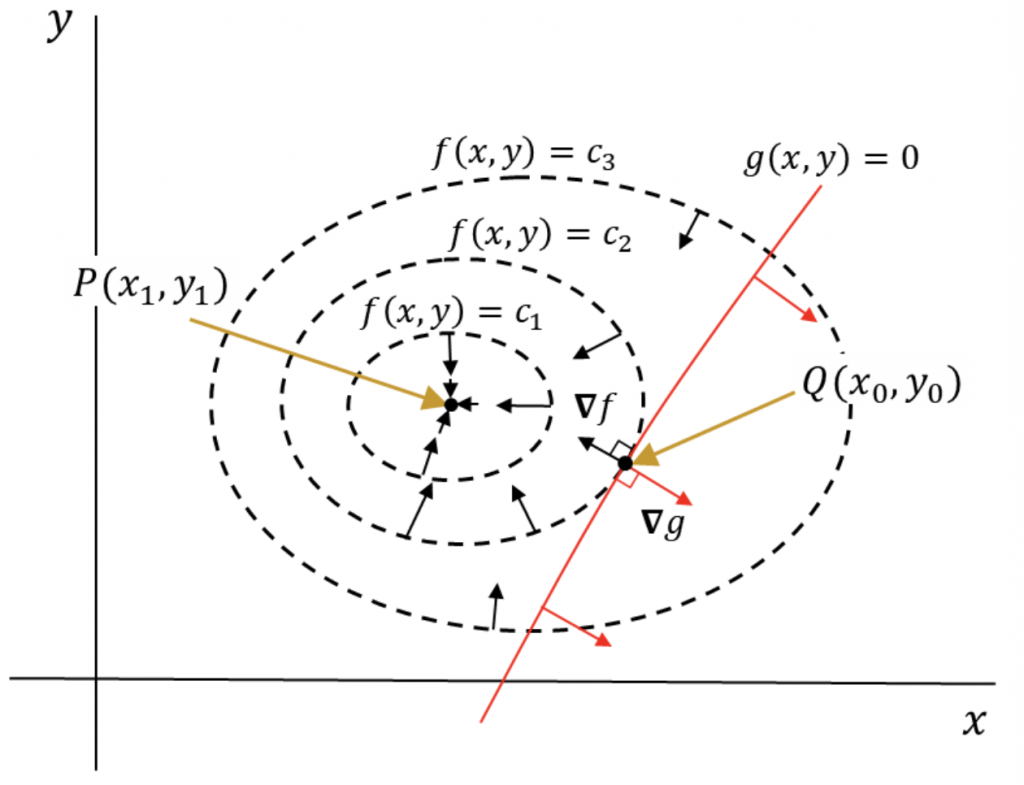
　図2．拘束条件のある極値（2変数）。(上図）はの拘束条件のもとQで極値をとる（条件がない場合はPで極値）（下図で、黒矢印は、赤矢印は。Qでとは一直線上にあるので、(5)が成り立つがあります。）

 

C4. ベクトル微分の公式

のとき、

 

と定義します。

特に、とすると、より、

 

また、

（は対称行列）とすると、より