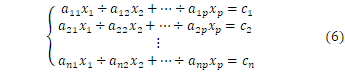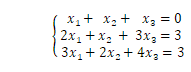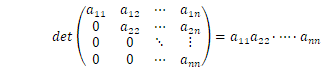誤差論と最小二乗法
第8回付録 線形(線型)代数の基礎2
2020年03月18日
A2. 行列の演算
一次(線形)写像
は、![]() 次元ベクトル
次元ベクトル![]() を
を![]() 次元ベクトル
次元ベクトル![]() へ写すということを示しています。これを一次(線形)写像といいます。
へ写すということを示しています。これを一次(線形)写像といいます。![]() の時に一次変換という場合もあります。
の時に一次変換という場合もあります。
を二次形式といいます。値はスカラー(数)です。![]() が対称でない正方行列だとしても
が対称でない正方行列だとしても
ですから、
となり、二次形式は常に対称行列で書けることがわかります。
正定値行列
対称行列![]() がすべての
がすべての![]() に対して、
に対して、![]() となるとき、正定値といいます。また、
となるとき、正定値といいます。また、![]() となるとき半正定値といいます。
となるとき半正定値といいます。
以下の定理があります。![]() が正定値なら、その対角成分
が正定値なら、その対角成分![]()
![]() が半正定値なら、その対角成分
が半正定値なら、その対角成分 ![]()
また、
![]() を
を![]() 正定値行列、
正定値行列、![]() を
を![]() 行列としたとき、
行列としたとき、![]() ならば、
ならば、![]() は正定値 (5a)
は正定値 (5a)![]() または
または![]() ならば、
ならば、![]() は半正定値 (5b)
は半正定値 (5b)
です。
(参考) 共分散行列は正定値または半正定値ですが、半正定値となるのは変数間に線形関係があるときに限られます。
例. 二つの確率変数に常に![]() という関係があるとしましょう。
という関係があるとしましょう。![]() と書けるので、
と書けるので、![]() の共分散行列は
の共分散行列は![]() の分散
の分散![]() から誤差伝播により、
から誤差伝播により、
となります。この共分散行列は、二次形式を作ると
![]()
であり、![]() の時は0となるので半正定値です(上記(5b)の場合)。
の時は0となるので半正定値です(上記(5b)の場合)。
連立一次方程式
は行列の形に書けます。
と求まります。
一般に、![]() なら方程式の数が未知数の数より多いので解は存在しません。
なら方程式の数が未知数の数より多いので解は存在しません。![]() なら解は無限に存在します。次の定理があります。
なら解は無限に存在します。次の定理があります。
例1.
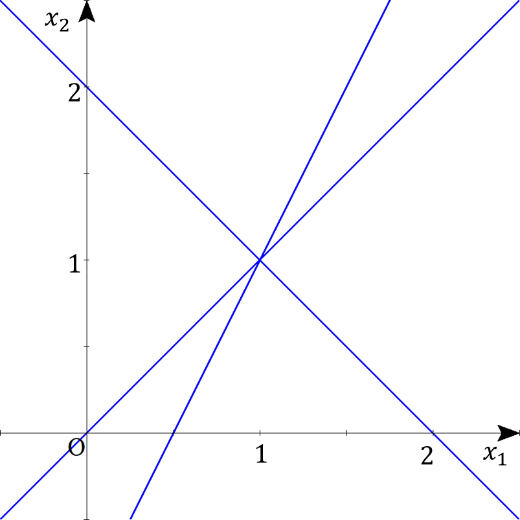
![]() です。従って解をもちます。第3式×2+第2式=第1式×3ですから、実は1式は不要で解は一意に決まります(図1)。
です。従って解をもちます。第3式×2+第2式=第1式×3ですから、実は1式は不要で解は一意に決まります(図1)。
例2.
![]()
![]() の列は一次独立で、
の列は一次独立で、![]() となり、解を持ちません(図2)。このような場合、近似的に最適な解は、最小二乗法により
となり、解を持ちません(図2)。このような場合、近似的に最適な解は、最小二乗法により
を最小にすれば求めることができます。
図2.解なし
例3.
![]() で第1式と第2式を足すと第3式になるので、実質2式であり
で第1式と第2式を足すと第3式になるので、実質2式であり![]() となり解をもちます。第1,2式より
となり解をもちます。第1,2式より
と表せるので、解は、
行列式
![]() 行列
行列![]() の行列式は、各行と列から1つずつ行列要素をとって掛け合わせ足した関数で次のように定義され、
の行列式は、各行と列から1つずつ行列要素をとって掛け合わせ足した関数で次のように定義され、![]() または
または![]() と書きます、
と書きます、
ここで![]() は
は![]() の並べ替え(置換)で、和はすべての置換について取り、符号は置換が偶なら正、奇なら負となります(置換はもとの
の並べ替え(置換)で、和はすべての置換について取り、符号は置換が偶なら正、奇なら負となります(置換はもとの![]() から2つずつ何回か入れ替えると得られますが、その回数が偶数なら偶置換、奇数なら奇置換といいます)。例えば、
から2つずつ何回か入れ替えると得られますが、その回数が偶数なら偶置換、奇数なら奇置換といいます)。例えば、
行列式には次のような性質があります。![]() が正則でない⇒
が正則でない⇒![]() 、
、![]() が正則⇒
が正則⇒![]()
また、正則な行列![]() の逆行列は行列式を使って次のように書けます。
の逆行列は行列式を使って次のように書けます。
B. 多次元正規分布の確率密度関数
多次元の正規分布は以前にも紹介しましたが、ベクトルと行列で表示すると便利であるとともに変数の関係などが見えやすいのでここにまとめておきます。
標準化(平均=0、分散=1)された![]() 個の独立な正規分布確率変数
個の独立な正規分布確率変数![]() があるとします。その時の同時確率密度関数は、
があるとします。その時の同時確率密度関数は、![]() として、
として、
となります。
C. テイラー展開
![]() (
(![]() )を滑らかな(何回でも微分可能な)実数値関数とし、
)を滑らかな(何回でも微分可能な)実数値関数とし、![]() を
を![]() の近傍の点とすると
の近傍の点とすると
と表されます。![]() は滑らかな関数です。第3項は
は滑らかな関数です。第3項は![]() の二次になっていますから、
の二次になっていますから、![]() が小さいとすると無視することができ
が小さいとすると無視することができ
となり![]() の線形式で書けることがわかります。測量では、未知数と観測量の関係が線形でないとき、テイラー展開を使って線形化するのが一般的です。
の線形式で書けることがわかります。測量では、未知数と観測量の関係が線形でないとき、テイラー展開を使って線形化するのが一般的です。