連載
第3回 地球基準座標系
2017年07月19日
3.地球座標系
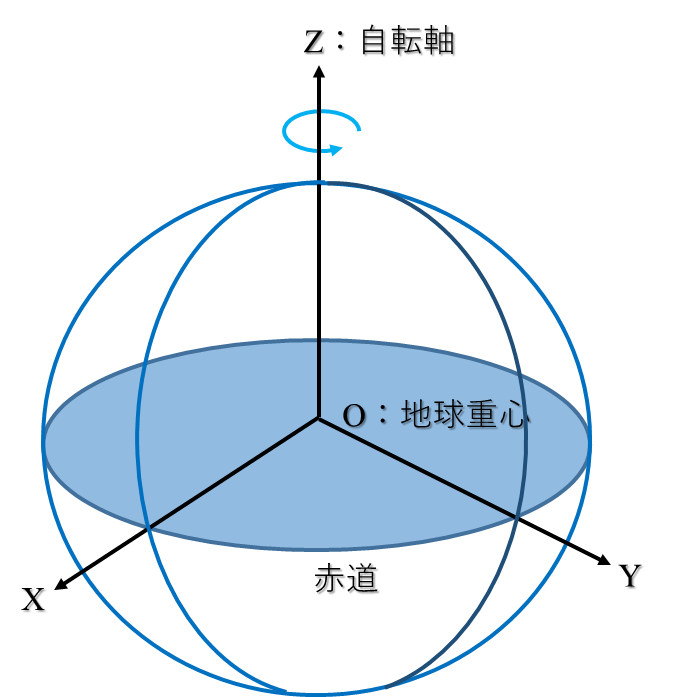
今回から地球上の位置を表す座標系(特にITRS/ITRF)についてお話ししましょう。前回、時間軸も含めたGTRSを紹介しましたが、今回は3次元直交座標系を考えます。3次元座標系は、原点と3軸の方向(と長さの単位)を定義すれば決まりますが、地球全体が対象で衛星測位に便利なものといえば、原点は地球中心(重心)、軸の方向は赤道系(つまり、Z軸は極方向でXY平面は赤道面)である座標系を導入すればよいでしょう(図1)。そのような座標系は、宇宙開発が始まった20世紀後半からいくつか作られてきました。アメリカ国防総省によるWGS 84(とそれ以前のWGS 72など)は最も有名です。国際機関による取り組みでは、第1回でも述べましたがIERS(及びその前身であるBIH:国際報時局)が複数の宇宙測地技術を使って正確な座標系の構築を進めてきました。その地球基準系がITRS/ITRFで、現在では世界標準となっています。
IUGGは、後追いの形ではありますが2007年の総会決議において、ITRSは過去のシステムとの連続性をもったGTRSの一つと考えられ、ITRSを地理情報やナビゲーションのために使われるべき座標系である、と公認しています。
3.1 ITRS
ITRSの定義は以下のとおりです。
- 地心系で原点は大気・海洋も含んだ地球の重心。
- 長さの単位はメートル(国際基本単位SI)。スケールは地心の座標時(TCG)にあわせたもの(注1)。
- 座標軸の向きは、1984.0のBIH基準系のものを初期値とする(注2)。
- 座標軸の向きの時間変化はプレート運動のNNR(no-net-rotation)の条件に従う。
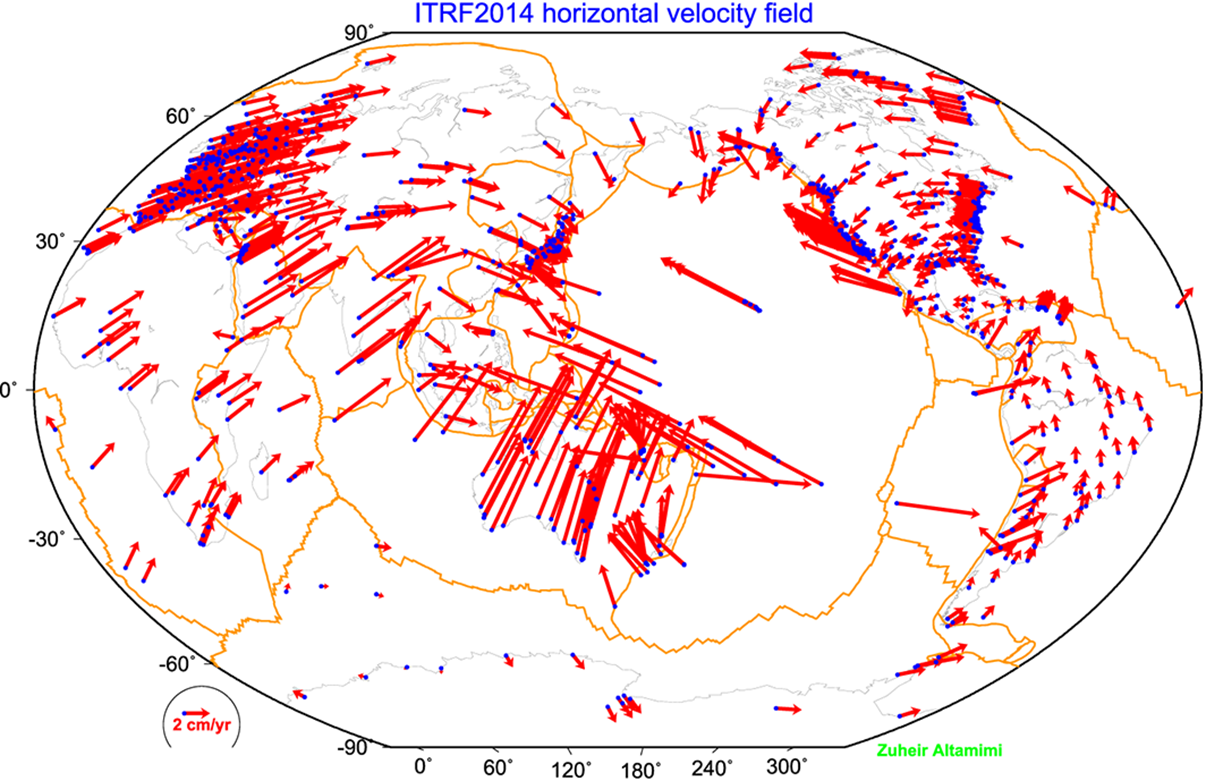
GTRSは4次元座標系ですが、ITRSは3次元なのでGTRSの空間部分と考えてよく、さらに以前のBIH座標系と連続性をもたせたものになっています。また、軸は地球固定(正確には地殻)ですが、プレート運動のため地殻は動きます。定義の4.のNNRとは、地球上のプレートの回転速度(正確には角運動量)を全て足すと0になるように座標系の向きが決められるという条件で、時間がたっても座標系が地殻に関して回転しないように保証しています。
(注1)1メートルの定義は、光が真空中で秒間に進む距離です。従って重力ポテンシャルの違いによって時間の進みが違うとこの距離も違ってきます。
(注2)BIHは、1984年から宇宙測地技術観測データを使って基準座標系の構築を進めてきました。最初の座標系では、BIHが事業の一つとして提供している地球回転パラメータの値から座標軸の向きを決定しました。
3.2 ITRF
ITRSの実現として、具体的に基準点の位置及び速度を与えたものがITRFです。
3.2.1 ITRFの特徴
(1)複数の宇宙測地技術を統合して解を求めたもの
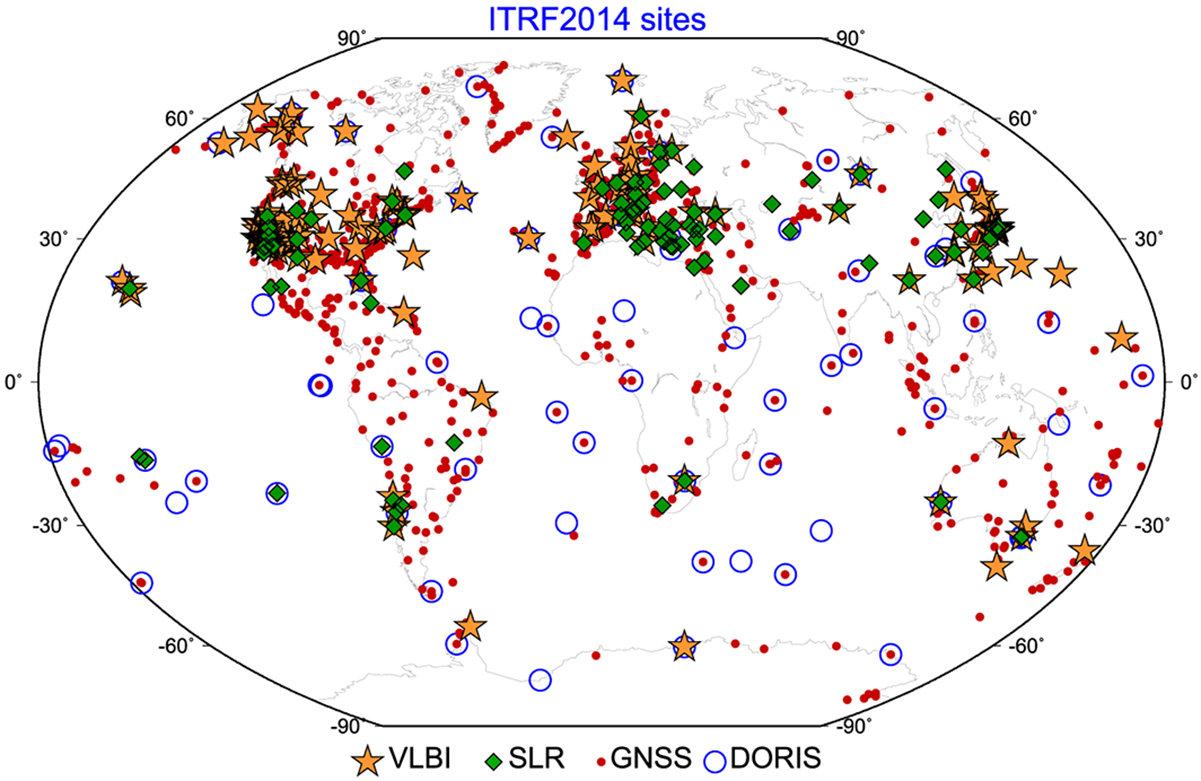
4つの宇宙測地技術、GNSS、VLBI、SLR、DORISの国際観測結果から解を算出しています。一つの技術だけでは地球座標系に必要なパラメータを算出することはできません。また、各技術には強みと弱みがあります。ITRFは4つの技術の特徴を生かしながら弱点を補っているため正確な座標系の構築が可能になっているのです。
(2)ダイナミックな座標系
ITRFは元期での基準点の位置と速度を与えます。従って、を基準の元期とすると、ある時期における基準点の位置は以下のようにあらわされます。
ここで、![]() は元期での位置、
は元期での位置、![]() は元期での速度です。
は元期での速度です。
(3)数年ごとに改定
地球は常に変動していますので、正確な位置と速度を提供するためには、最新のデータをとりこんで計算を繰り返し更新してゆく必要があります。これはITRFがまず科学的用途を念頭に入れているからです。
3.2.2 計算の概要
ITRFは、IGSなどの各宇宙測地事業の解析センター(複数)が提出した解を結合したものです。それらの解は、長期間(10~30年)にわたるグローバルな観測から決めた各基準点の位置と速度です。また、結合の際には複数の観測技術を持つ局でのコロケーション測量が必要です。コロケーション測量とは、同じ観測局内にある異種観測点間の位置ベクトルを精密に求めるための測量です。結合の計算の詳細は省略しますが、原点(地球重心)は主にSLR観測から、スケールはSLRとVLBIの観測から決定されています。
ITRFにおける基準点の位置・速度の正確さは、もちろん観測技術と観測期間によって異なりますが、オーダーとして位置は数mm、速度は0.1 – 0.5mm/年となっています。
3.2.3 歴史
IERSは1984年から地球基準系の構築を進めてきました。ITRFとしては最初のITRF88から最新のITRF2014まで13のフレームが実現されています。
観測ネットワークも進化しています。ITRF88 は、VLBIとレーザー測距観測のみで構築されました。その後GPSとDORISが加わり現在の4つの宇宙技術による観測ネットワークが完成しています。
観測局数はITRF88の約160局(コロケーション数は22)からITRF2014では1499局(139コロケーション)に増大し、正確な地球座標系が実現されています(図1-3)。
3.3 ITRFと他の地球基準座標系
上でも述べたように、ITRFは最も正確な地球基準座標系として世界標準となっています。GPSが準拠するWGS84は何回かの改訂を経て、現在ではITRFとの差が㎝レベル以下となり、実用上同じものと考えて支障ありません。ただし、ITRFのWebsiteは、WGS84とITRFに関する公式の変換パラメータは存在しないとしています。日本の測地系は世界測地系への移行の際、ITRF94の元期1997.0での値に準拠して基準点成果を決定しました(なお、2011年東北地方太平洋沖地震後の東日本1都19県は、ITRF2008(元期2011.4)を採用しています。)。オーストラリアやニュージーランド、韓国、マレーシアなどのアジア諸国もITRFに準拠して自国の測地座標系を構築しています。ITRFと他の基準系との関係は、後日また紹介したいと思います。
略語集
BIH Bureau International de l’Heure 国際報時局
DORIS Doppler Orbitography and Radioranging Integrated by Satellite
GNSS Global Navigation Satellite System 全球測位衛星システム
ITRS/ITRF International Terrestrial Reference System/Frame 国際地球基準座標系
SLR Satellite Laser Ranging 衛星レーザー測距
TCG Geocentric Coordinate Time 地心座標時
VLBI Very Long Baseline Interferometry 超長基線電波干渉計
参考文献
- Boucher, C, Z. Altamimi (1990), Evolution of the realizations of the Terrestrial Reference System done by the BIH and IERS (1984-1988), IERS Technical Note No. 4, Observatoire de Paris.
- Altamimi, Z., P. Rebischung, L. Metivier, and C. Xavier (2016), ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions, J. Geophys. Res. Solid Earth, 121, 6109?6131, doi:10.1002/2016JB013098.