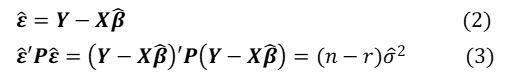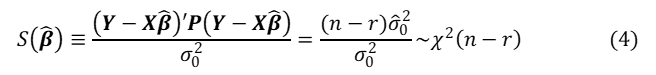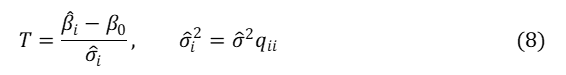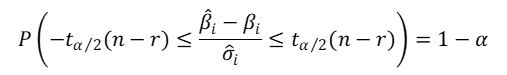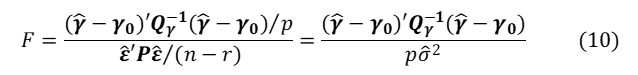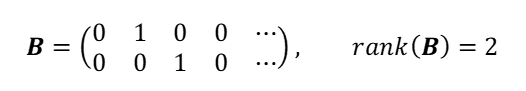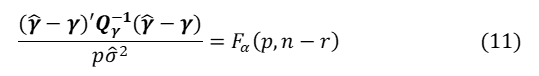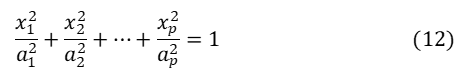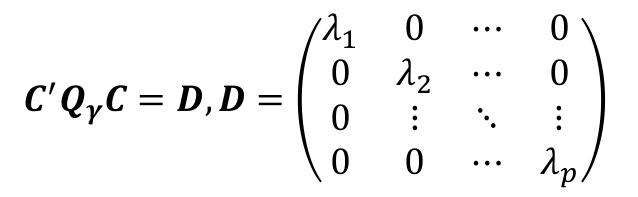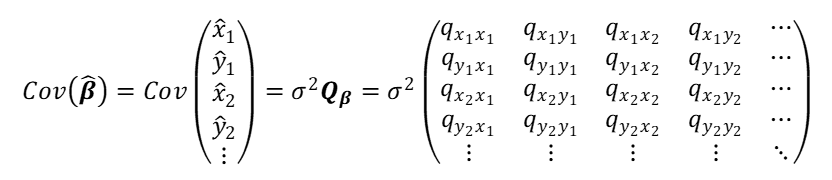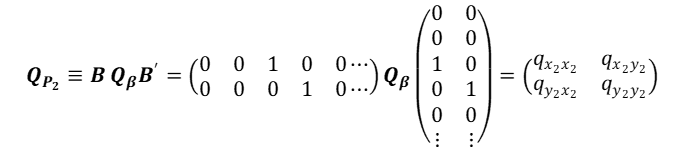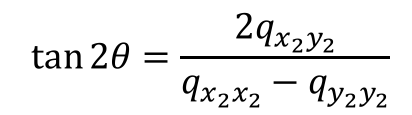誤差論と最小二乗法
第9回 最小二乗解の誤差と検定
2020年06月10日
最小二乗解が計算できると、残差、基準分散の推定値、解の誤差行列も得られますので、それらによりモデルも含めた最小二乗問題の評価をすることができます。ただし、具体的な計算をするためにデータの誤差は正規分布に従うと仮定します。
今回は考え方と式を導き、具体的な計算例については次回ご紹介したいと思います。
1.残差と残差二乗和
残差とその(重み付き)二乗和(第7,8回参照)
は、測定値と計算値の対応の良さを見る一つの目安となります。
基準分散![]() が既知の場合
が既知の場合![]() は、残差二乗和を基準分散で割った量が自由度
は、残差二乗和を基準分散で割った量が自由度![]() の
の![]() 分布(第5回)に従うことがわかっています。
分布(第5回)に従うことがわかっています。
最小二乗法によるあてはめに問題なければ、![]() あるいは
あるいは![]() となるはずなので、ここでは、帰無仮説
となるはずなので、ここでは、帰無仮説![]() を
を
として有意水準αで両側検定を行うことにしましょう。![]() を計算し、
を計算し、
ならば、仮説は棄却されません。もし、棄却すべきとの結果になれば、測定値あるいはモデルに問題があるとして再検討しなければなりません。
検定の例として、技術顧問中根勝見による以下の論文を挙げておきます:
(測地学会誌 第63 巻 第2 号 Journal of the Geodetic Society of Japan (2018), 117-122 頁 Vol.63 , No 2, (2018), pp.117 -122)
2. 解の分散と誤差楕円
最小二乗解とその共分散(誤差)行列は、次のように求められました(第7、8回)。
2.1 パラメータの検定と信頼区間
2.1.1 1つのパラメータの検定と信頼区間
検定
パラメータの一つ に注目し、帰無仮説 と対立仮説![]() と対立仮説
と対立仮説![]() を
を
と設定して検定(![]() が
が![]() に等しいか否か)を行うことにします。このとき、統計量
に等しいか否か)を行うことにします。このとき、統計量
は、自由度![]() のt分布に従うことが分かっています。ここで、
のt分布に従うことが分かっています。ここで、![]() は基準分散の推定値、
は基準分散の推定値、![]() は
は
![]() の
の![]() 成分で、
成分で、![]() は解
は解![]() の分散の推定値となります。従って、平均値の検定(B2)と同じように行うことができます。
の分散の推定値となります。従って、平均値の検定(B2)と同じように行うことができます。
信頼区間
から
となります。
2.1.2 複数のパラメータ
F検定
複数のパラメータ![]() を同時に検定する場合は、F検定を用います。帰無仮説は、
を同時に検定する場合は、F検定を用います。帰無仮説は、
対立仮説は、
となります。帰無仮説は、![]() パラメータをある値に固定することに相当し、固定しない対立仮説との差をみるには、残差二乗和を比べ、次の統計量を計算します。
パラメータをある値に固定することに相当し、固定しない対立仮説との差をみるには、残差二乗和を比べ、次の統計量を計算します。
ここで、![]() は最小二乗解の残差二乗和、
は最小二乗解の残差二乗和、![]() はγに対応する
はγに対応する![]() の部分行列(注)で、分子はγの推定値と検定値との差の二乗和になっています。帰無仮説が正しいときに、Fは自由度
の部分行列(注)で、分子はγの推定値と検定値との差の二乗和になっています。帰無仮説が正しいときに、Fは自由度![]() のF分布
のF分布![]() に従うので、F検定を行うことができます。有意水準αとしてパーセント点を求め、
に従うので、F検定を行うことができます。有意水準αとしてパーセント点を求め、
なら、仮説は棄却されます。対立仮説が正しいとすると、Fは差の二乗和で必ずある正数以上ですから、片側検定となります。
(注)![]() と書け、Bは第j列から第k列までが単位行列をなし、他は0なのでランクはpとなり、
と書け、Bは第j列から第k列までが単位行列をなし、他は0なのでランクはpとなり、![]() は正定値で逆を持ちます(第8回A2参照)
は正定値で逆を持ちます(第8回A2参照)
で
です。
信頼領域と誤差楕円
この式はパラメータの信頼領域を表しており、パラメータの二次式ですから、![]() を中心とした楕円体の形をしていることが分かります。
を中心とした楕円体の形をしていることが分かります。
楕円体の標準的な方程式は、
なので、(11)をこの形に変換すれば楕円の大きさや軸の向きが分かります。そのために![]() を直交行列Cで対角化(付録A3参照):
を直交行列Cで対角化(付録A3参照):
して
とおくと、
となります。対角要素は![]() の固有値、Cの列ベクトルは、各固有値に対応する固有ベクトルになります。
の固有値、Cの列ベクトルは、各固有値に対応する固有ベクトルになります。
従って、(11)は
を各軸の半径とする楕円体となります。Cの列ベクトルの方向が楕円体の軸の方向になります。
特に、![]() のとき、誤差楕円(体)と呼びます。従って、誤差楕円の各軸の長さは、
のとき、誤差楕円(体)と呼びます。従って、誤差楕円の各軸の長さは、![]() です。
です。
例.2次元の基準点測量
未知パラメータは未知点![]() の座標
の座標![]() です。点
です。点![]() の誤差楕円を求めてみましょう。解の誤差行列を
の誤差楕円を求めてみましょう。解の誤差行列を
から計算できます。計算の詳細は省略しますが、固有多項式を解いて(A3参照)、
また、![]() に対応する固有ベクトルを
に対応する固有ベクトルを![]() とし、
とし、![]() とx軸との角度をθとすると、
とx軸との角度をθとすると、
です。誤差楕円は図1のようになります。
図1.誤差楕円