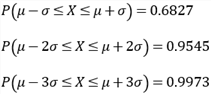誤差論と最小二乗法
第3回 – いろいろな確率分布
2019年09月06日
今回は、前回紹介した確率分布の実際の例をいくつか見ていきたいと思います。
1.離散型の確率分布
1.1 二項分布
成功か失敗かの二つの結果が出る実験を考えます。成功の確率を![]() とすれば、失敗の確率は
とすれば、失敗の確率は![]() となります。この実験を独立に(つまり、前後に関連性はなく)
となります。この実験を独立に(つまり、前後に関連性はなく) ![]() 回繰りかえした時,
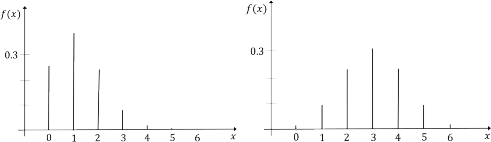
回繰りかえした時,![]() 回成功する確率分布が二項分布です(図1)。
回成功する確率分布が二項分布です(図1)。
と展開してみると、![]() 回成功すればのこりの
回成功すればのこりの![]() 回は失敗ですからすべての場合の確率を足すと1となり、(1)が確率分布を与えることがわかります。
回は失敗ですからすべての場合の確率を足すと1となり、(1)が確率分布を与えることがわかります。
二項分布の平均、分散は、
です。
1.2 一様分布
サイコロを振った時に出る目の確率はどの目でも同じです。このような確率分布を離散一様分布といいます(図2)。
サイコロの場合は、N=6です。
指数分布の平均と分散は、それぞれ
となります。
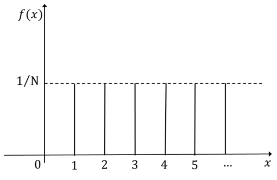
図2. 一様分布
2.連続型の確率分布
2.1 正規分布
正規分布は、統計学において最も重要な分布関数です。ガウスが導いた誤差関数に由来するのでガウス分布とも呼ばれ、測量の分野では最も多く使われています。
正規分布の密度関数は、
![]()
この密度関数から、平均と分散を計算すると、
![]()
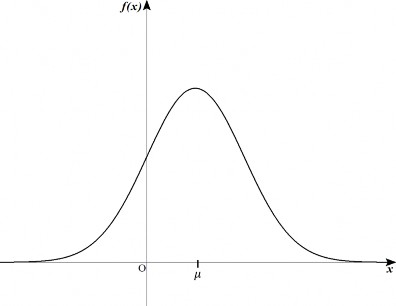
となるので、正規分布(3)は平均値と分散で決まり、![]() と表します。グラフを書くと、平均値のときが最大で左右対称となるおなじみの釣り鐘型の形をしています(図3)。また、平均値が0、分散が1の正規分布を標準正規分布といい
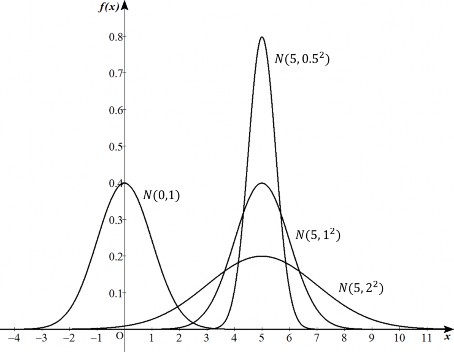
と表します。グラフを書くと、平均値のときが最大で左右対称となるおなじみの釣り鐘型の形をしています(図3)。また、平均値が0、分散が1の正規分布を標準正規分布といい![]() と書きます(図4)。
と書きます(図4)。
正規分布の場合、基本的な区間確率がよく使われます。確率変数![]() が
が![]() に入る確率を
に入る確率を![]() とすれば、
とすれば、
となり、値が標準偏差![]() 内に落ちる確率は約68.3%、
内に落ちる確率は約68.3%、![]() 内に落ちる確率は約95.4%、
内に落ちる確率は約95.4%、![]() 内に落ちる確率は約99.7%です。
内に落ちる確率は約99.7%です。![]() 範囲を外れることは極めて起こりえないと判断されます(図5)
範囲を外れることは極めて起こりえないと判断されます(図5)
正規分布は、統計学において他の分布の近似や統計的推定など多くの場合に利用されています。その正当化の大きな理由が次の中心極限定理です。
中心極限定理:ある適当な確率分布を持ったn個の独立な確率変数があるとき、それらの和は(一般的な条件の下で)、nが大きくなれば正規分布に従うようになる。
この定理により1.1で述べた二項分布は、nが大きい時正規分布に近づきます。また、実験や計測におけるランダム誤差は、独立で小さな誤差が多数集まって生じると考えてよい場合、正規分布(及びその多次元分布(次回))を仮定することが多いのです。
ただし、実際の分布でそのまま正規分布となるものは、測定誤差や生物測定(身長・体重など)などを除けばそれほど多くはありません。
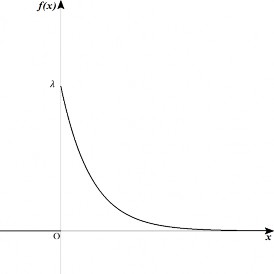
2.2 指数分布
確率密度関数
を持つ分布を指数分布といい、寿命や故障までの時間など待ち時間を表す時によく使われます(図6)。
平均、分散はそれぞれ、
![]()
となります。
次回は、多次元の確率分布についてです。