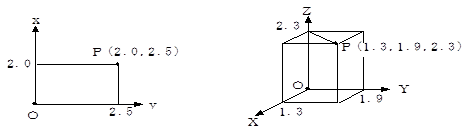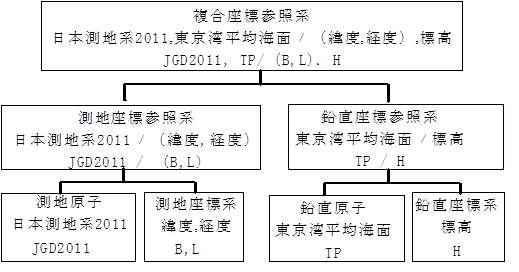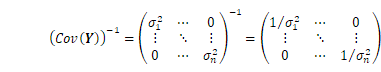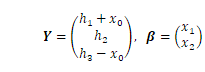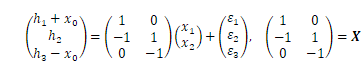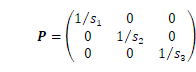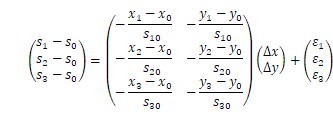「連載」について
「連載」について
2020年03月16日
「連載」では、当社技術顧問による連載記事を掲載します。
掲載記事一覧
『よくわかる測地成果2000』 |
技術顧問 中根勝見 |
『座標系講座』 |
技術顧問 松坂茂 |
『座標系講座 生活編』 |
技術顧問 中根勝見 |
『空間データの品質』 |
渡邉孝三 |
『空間データの品質向上』 |
渡邉孝三 |
『誤差論と最小二乗法』 |
技術顧問 松坂茂 |
技術顧問プロフィール
中根勝見プロフィール
1937年 |
東京都出身 |
1955年 |
建設省国土地理院 入省 精密基準点測量、水準測量 重力・地磁気観測、地殻変動解析 測量データ処理 途上国研修員教育等に従事 |
1963年 |
東京電機大学卒 |
1983-5年 |
ケニア共和国測地専門家 |
1997年3月 |
国土地理院(研究官)退職 |
現在 |
アイサンテクノロジー(株)技術顧問 博士(工学)技術士(応用理学) |
松坂茂プロフィール
1956年 |
千葉県出身 |
1982年 |
東京大学大学院理学系研究科修了 国土地理院入省 宇宙測地技術(主にVLBI)の開発・解析、 国際測地観測に従事 |
1990-91年 |
米国測地測量局在外研究員 |
1999-2007年 |
国際VLBI事業(IVS)評議員 |
2011年 |
IAG(国際測地学協会)フェロー |
2016年 |
国土地理院 退職 |
現在 |
アイサンテクノロジー(株) 技術顧問 |
渡邉孝三プロフィール
出身地 |
新潟県 |
1969年 |
東京電機大学卒業 |
1969年 |
武藤工業入社 CAD,GISシステムの開発、販売に従事 |
1988年 |
GIS学会設立に参加、設立後理事 |
1992年 |
NSDIPA設立に参加、設立後事務局次長 |
1996年 |
アジア航測株式会社入社、GISセンター長 |
2001年 |
株式会社NTTデータ入社、統合型GIS室長 自治体の統合型GISのコンサルタント |
2003年 |
「実学 自治体のための統合型GIS」出版 |
2008年 |
株式会社NTTデータ信越入社、統合型GIS室長 自治体の統合型GISのコンサルタント |
2010年 |
株式会社NTTデータ信越 顧問 アイサンテクノロジー株式会社 技術顧問(〜2015年) |
座標系講座 生活編
第1回 その1 – 測量法に基づく測量の基準
はじめに
連載「座標系講座」でお話ししましたように、衛星測位の高度化に伴って,地球上の正確な位置が容易に求まるようになりました。国民生活にとって、土地の境界や水道配管における高低差の把握は、位置を決める座標に基づいて設計されます。その地上の位置は、測量法第11条で定められた位置の基準に基づいて決められます。すなわち、衛星測位によってどんなに正確な位置情報であるcm級の座標を測定したところで、私たちの生活の場である地上での受け入れ態勢が整えられていなければ、有効な活用になりません。例えば、正確に作成されていない地図であれば、衛星測位の位置と地図上の位置がずれます。例えば、カーナビの地図が正確でなければ、衛星測位による自車の正確な位置は決められません。また、日本列島は年平均数cmに及ぶ地殻変動が生じています。大きい所では、時間経過によって精密単独測位(PPP)の位置が1m以上ずれてしまっています。
以上のように、正確な衛星測位は、測量法によって私たちの生活の場に活用されるようになります。以下、測量法上の位置の取り決めを中心に考察を行いたいと思います。
第1回 測量法に基づく測量の基準
測量法に基づく測量の基準は、明治時代における天文測量及び三角測量によって構築された「日本測地系(Tokyo Datum:TD)」及び衛星測位に基づく世界測地系である「日本測地系2000(Japanese Geodetic Datum 2000 : JGD2000)」があります。更に、2011年東北地方太平洋沖地震後に更新された「日本測地系2011(Japanese Geodetic Datum 2011 : JGD2011)」があります。以下にこれらの解説を行うことにします。
1. 日本測地系の測量法第11条(測量の基準)
最初につくられた測量法(昭和24年法律188号)は、古い測量技術である天文測量及び三角測量によって位置が決められました。測量法第11条は、①地球の大きさとしてベッセル楕円体の長半径6,377,397.155m及び扁平度1/299.152813を定め ②座標系として楕円体座標系及び平均海面からの高さを定め ③測量の出発点である原点の地点として日本経緯度原点(東京都港区麻布台)及び日本水準原点(東京都千代田区永田町)を定め、その数値は測量法施行令で定めました。施行令第2条は、①日本経緯度原点の緯度、経度及び鹿野山一等三角点の方位角を定め ②日本水準原点の東京湾平均海面からの高さを定めました。これらの内水平位置は、「日本測地系(Tokyo Datum)」と呼ばれています。
1.1 日本測地系の日本経緯度原点の緯度及び経度の偏り
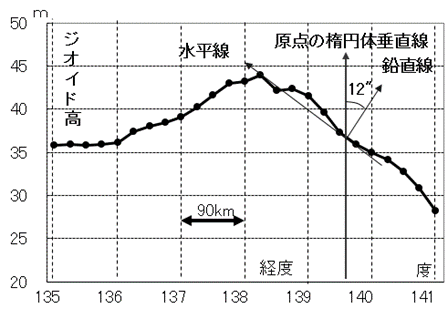
上記に示した日本経緯度原点の「測地原子」である緯度及び経度は、水平面に直交する重力の方向である鉛直線を基準とした天文測量に基づいたものです。日本経緯度原点において、重力による鉛直線と楕円体の垂直線が一致すると仮定し、天文緯度及び経度が、楕円体面上の緯度及び経度とされました。天文緯度及び経度に対して、楕円体面上のそれは測地緯度及び経度と呼びます。しかし、日本海溝の影響等で日本経緯度原点がある東京付近の重力方向は大きく傾いていました。すなわち、日本経緯度原点付近は水準面であるジオイド傾斜が大きい位置にありました。図1及び図2は、日本経緯度原点を通過する南北(緯度)及び東西方向(経度)のジオイド高を示したものです。日本経緯度原点付近の楕円体面に対する水平面であるジオイドの傾きは、緯度及び経度共に約12秒でした。
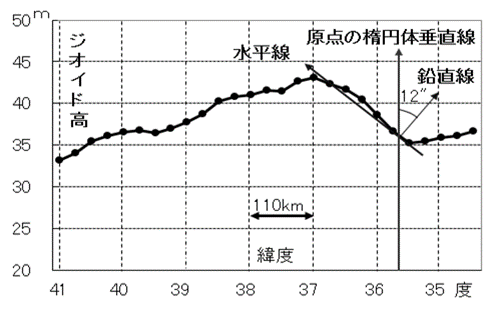
図1 日本経緯度原点のジオイド傾斜(緯度)
図2 日本経緯度原点のジオイド傾斜(経度)
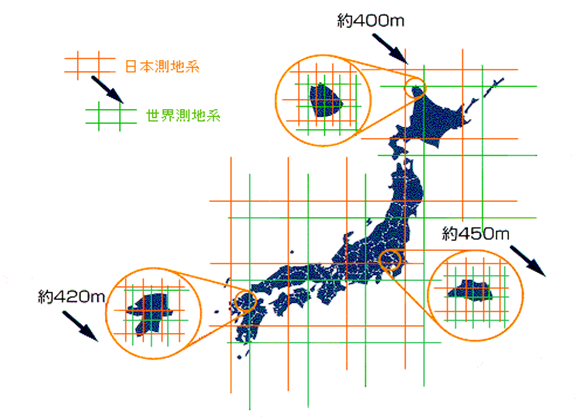
図3に示す日本測地系の日本経緯度原点の位置のずれ(偏り)450mは、次の概略計算に示すように、鉛直線偏差による影響が主要な原因です。
・南北方向のずれ=子午線曲率半径(6355000m)×12秒/206265秒=370m
・東西方向のずれ=卯酉線曲率半径(6385000m)×12秒×cos(緯度)/206265秒=300m
・合計のずれ=√{3702+3002}=476m
図3 日本測地系の位置のずれ(国土地理院による)
1.2 日本測地系の三角網
図4に示すように、1883年から開始された一等三角測量は、日本経緯度原点を出発点として、関東及び遠州地方の三角網が決められ、その三角網は日本全国へ延長されました。この測地基準系は、既に述べましたように、「日本測地系(Tokyo Datum)」と呼ばれているものです。
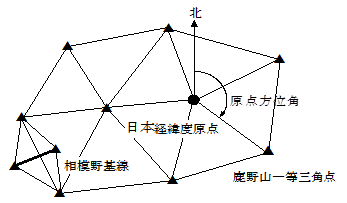
図4 武遠三角網(経緯度原点、鹿野山一等三角点、相模野基線)
1.3 日本の鉛直基準座標系(標高系)
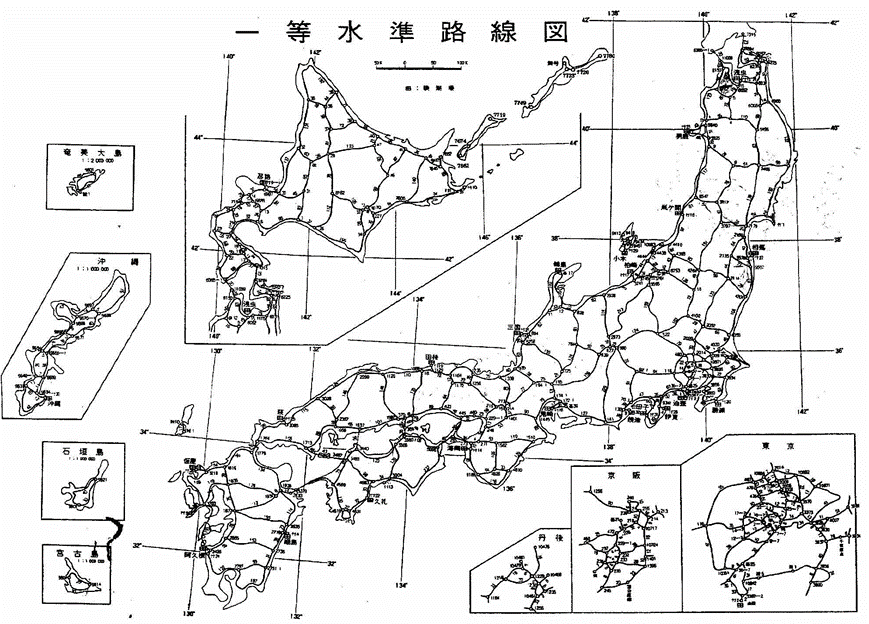
一方、高さは、図5に示す国道沿いに配置された一等水準測量網が、明治16(1883)年から、当時の陸地測量部により組織的に開始されました。それ以降9回余りの繰り返し測量が行われてきました。水準点は、主要国道沿いに約2km間隔で設置されていて、現在約1.4万点が、国土地理院によって管理・運営されています。これらの水準点を基準として各地の高さが決められてきています。
図5 一等水準測量網(国土地理院による)
一等水準測量等水準測量の成果に基づいて三角点の標高が決められました。三角点標高は、距離及び高度角により決められ、水準測量の成果より正確さに欠けるものです。
以上が、「日本の鉛直基準系(標高系)」です。
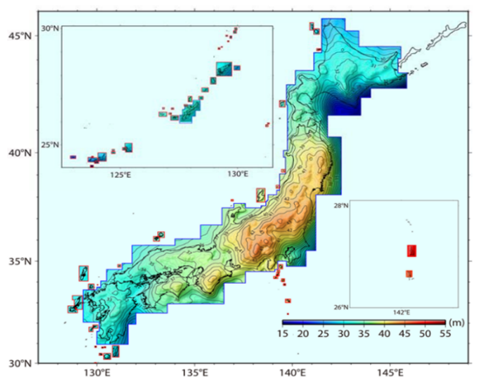
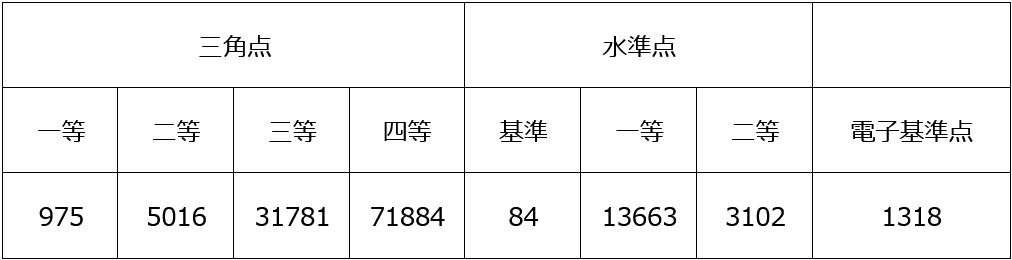
現在、国土地理院が管理している三角点等の基準点は表1のとおりです。
表1 国土地理院が管理する三角点等の基準点数(2018年4月1日現在)
http://www.gsi.go.jp/common/000188855.pdf
2. 世界の測量の基準
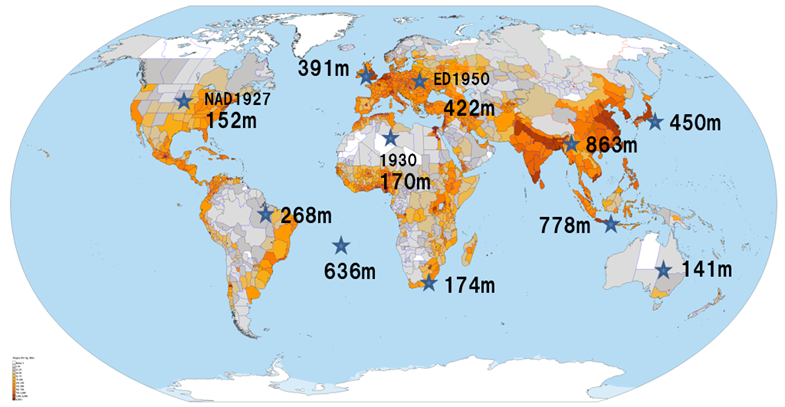
衛星測位になる前の天文測量による測量の基準は、100m単位のずれが生じていました。図 6は、米国のGPS測量により確かめた世界の主な国の測地基準座標系の誤差です。
図6 米国のGPS測量により確かめた世界の主な国の測地基準座標系の誤差
出典:DMA(Defense Mapping Agency) Technical Report,1987
世界の約3割の国(アジア地域では約5割の国々)では、今でも地球上の位置の基準がずれていて、衛星測位で計測した位置と地図上の位置が一致しません。そのため、2015年2月26日に、その改善を目的とした国連総会決議が行われました。測量の分野では初の決議ということです(参考文献1.宮原伐折羅,2015 )。
『第1回 その2 – 測量法に基づく測量の基準』へ
座標系講座 生活編
第1回 その2 – 測量法に基づく測量の基準
3. 日本測地系2000(JGD2000)の日本経緯度原点の測地原子
測量法の改正(平成13年6月、法53)により、第11条の測量の基準は、次に示す世界測地系の定義を定めました。
第十一条 基本測量及び公共測量は、次に掲げる測量の基準に従って行わなければならない。
| 一 | 位置は、地理学的経緯度及び平均海面からの高さで表示する。ただし、場合により、直角座標及び平均海面からの高さ、極座標及び平均海面からの高さ又は地心直交座標で表示することができる。 |
| 二 | 距離及び面積は、第三項に規定する回転惰円体の表面上の値で表示する。 |
| 三 | 測量の原点は、日本経緯度原点及び日本水準原点とする。ただし、離島の測量その他特別の事情がある場合において、国土地理院の長の承認を得たときは、この限りでない。 |
| 四 | 前号の日本経緯度原点及び日本水準原点の地点及び原点数値は、政令で定める。 |
| 2 | 前項第一号の地理学的経緯度は、世界測地系に従って測定しなければならない。 |
| 3 | 前項の「世界測地系」とは、地球を次に掲げる要件を満たす扁平な回転楕円体であると想定して行う地理学的経緯度の測定に関する測量の基準をいう。 |
| 一 | その長半径及び扁平率が、地理学的経緯度の測定に関する国際的な決定に基づき政令で定める値であるものであること。 |
| 二 | その中心が、地球の重心と一致するものであること。 |
| 三 | その短軸が、地球の自転軸と一致するものであること。 |
上記の定義に基づいて同施行令は、次に示す日本経緯度原点の緯度、経度及び原点方位角(第2条第1項)並びに楕円体要素(第3条)の測地原子を定め、更に、日本水準原点の標高である鉛直原子(第2条第2項)を定めています。
(日本経緯度原点及び日本水準原点)
| 第2条 | 法第11条第1項第4号に規定する日本経緯度原点の地点及び原点数値は、次のとおりとする。 |
| 一 | 地点 東京都港区麻布台二丁目18番1地内日本経緯度原点金属標の十字の交点 |
| 二 | 原点数値 次に掲げる値 |
| イ | 経度 東経139度44分28秒8869 |
| ロ | 緯度 北緯35度39分29秒1572 |
| ハ | 原点方位角 32度20分46秒209(前号の地点において真北を基準として右回りに測定した茨城県つくば市北郷1番地内つくば超長基線電波干渉計観測点金属標の十字の交点の方位角) |
| 2 | 法第11条第1項第4号に規定する日本水準原点の地点及び原点数値は、次のとおりとする。 |
| 一 | 地点 東京都千代田区永田町一丁目1番2地内水準点標石の水晶板の零分画線の中点 |
| 二 | 原点数値 東京湾平均海面上24.3900メートル (長半径及び扁平率) |
| 第3条 | 法第11条第3項第1号に規定する長半径及び扁平率の政令で定める値は、次のとおりとする。 |
| 一 | 長半径 6378137メートル |
| 二 | 扁平率 298.257222101分の1 |
上記の日本経緯度原点の緯度、経度及び原点方位角は、ITRF94の観測点である鹿島VLBI観測点の位置(元期1997.0)を基に電子基準点網を経由して決定されたものです。ここでは、三角測量時代と同様に、原点方位角が規定されていますが、楕円体高は規定されていません。衛星測位の測量の出発点では、原点方位角は不要ですが、緯度及び経度と共に楕円体高が必要なものです。ただし、測量法第11条に定められた地心直交座標系の原点座標(X,Y,Z)は、平成14年国土交通省告示第185号により定められていて、楕円体高の算出が可能です。
電子基準点網の原点に相当する鹿島VLBI点は、ITRF94に結合されているので、電子基準点の楕円体高は、全て決定することができます。
4. 日本測地系から世界測地系への座標変換
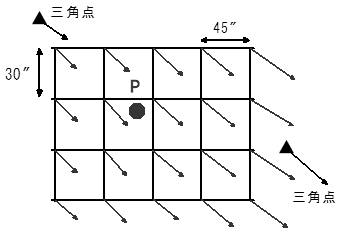
日本測地系と世界測地系の位置のずれは、図3に示されているように400m余りです。従いまして、日本測地系の座標で作られた地図等は、世界測地系の座標へ変換しなければ、衛星測位との整合がとれません。そのため、国土地理院は、日本測地系から世界測地系への座標変換プログラム「TKY2JGD(ティーケイワイツージェイジーディ):Tokyo to JGD」を開発しました(参考文献2. 飛田,2002)。座標変換パラメータは、表1に示した一等から三等までの三角点約3.8万点から島部を除いた3.7万点を使いました。これらの 3.7万点の新旧座標差から約1km×1km(経度方向45″×緯度方向30″)の格子点上の座標差をクリギング法により内挿して求めました。これは、「TKY2JGD座標変換パラメータ」と呼ばれているものです。
図7 TKY2JGD 座標変換パラメータ
格子点上の矢印が座標変換パラメータを表す。
P点の座標は周囲4格子点のパラメータからバイリニア法により内挿する。
図8は、世界測地系へのTKY2JGD座標変換パラメータを使って算出した最大剪断歪図で、座標変換誤差を推定したものです。この最大剪断歪は、測量の角度誤差に相当し、60ppmを超える地域は、1級基準点測量の誤差の許容範囲を超えることを示しています。伊豆半島に見られる大きな歪は、主として火山活動に伴うものです。箱根火山の影響もみられます。東京都―神奈川県境の大きな歪は、神奈川県の網平均計算時期(1992年)と東京都の網平均時期(1993年)の違いによって生じた座標の不整合(約40cm)の結果です。房総半島の付け根のばらついた歪は、1923年関東地震の改測域と改算域の境界における座標の不整合です。この座標変換に伴う座標変換誤差の最大は、1m程度と推定できます。
図8 関東南部のTKY2JGD座標変換パラメータによる座標変換誤差(最大剪断歪)
国土地理院公開の座標変換パラメータを利用してアイサンテクノロジー社が図化
日本測地系時代に作成された地籍調査による地籍図は、TKY2JGDにより座標変換され世界測地系地図とされます。その他の地図例えばゼンリン地図は、日本測地系に基づいて作成されていますから、TKY2JGDにより座標変換が行われているものと推定できます。従いまして、地図作成誤差の他座標変換誤差も含まれ、衛星測位と地図のずれになっています。
5. セミ・ダイナミック測地系の導入
日本列島は、4つのプレートが交叉する地域で複雑な地殻変動の場にあります。日本測地系時代は、地殻変動の影響を考慮しない「スタティック測地系」でした。衛星測位による位置の高精度化に伴い、地殻変動の影響を無視することができなくなりました。ニュージーランドは、2000年からセミ・ダイナミック測地系を導入していましたが、日本は2010年からセミ・ダイナミックの導入を決めました。セミ・ダイナミック測地系は、異なった観測時期の成果を元期の位置で統一的に表示するもので、日本測地系2000では元期1997.0を採用しました。
5.1 セミ・ダイナミック補正
セミ・ダイナミック補正は、相対測位であるGNSSスタティック測位における地殻変動の歪を基線ベクトルに補正するものです。従いまして、地殻変動の歪の無い平行移動の地殻変動地域では、セミ・ダイナミック補正は零になります。
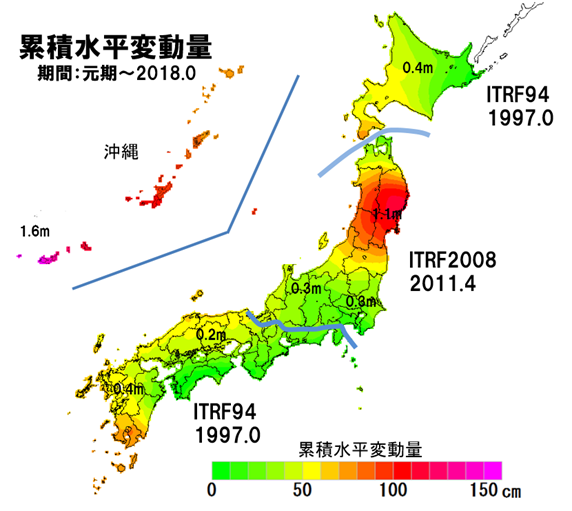
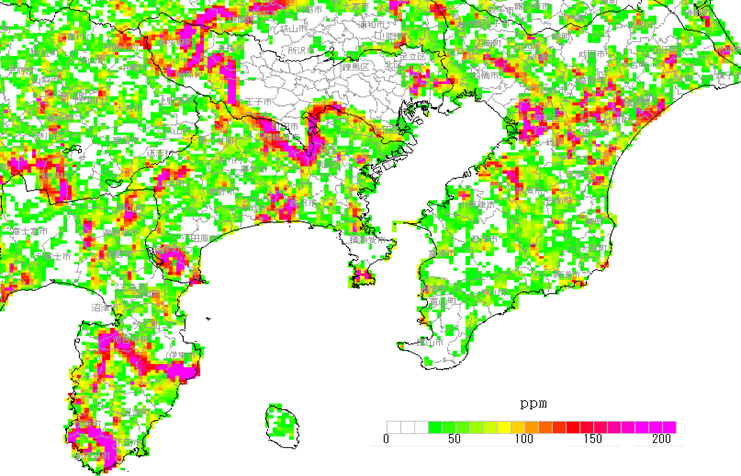
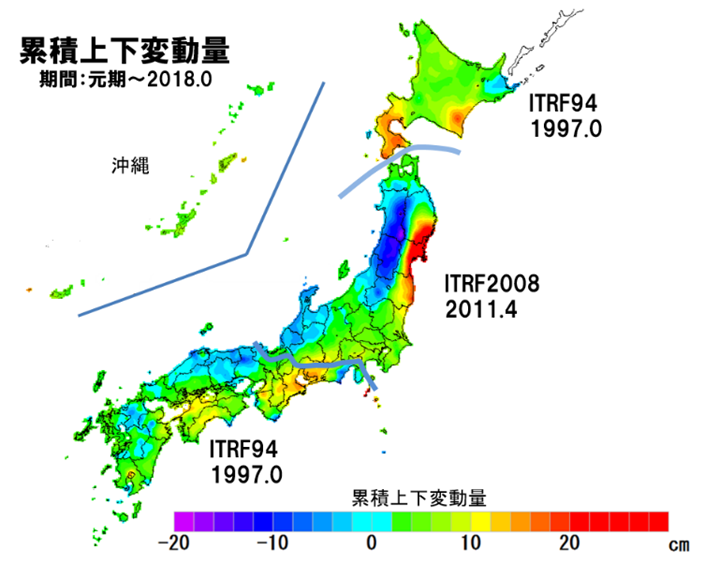
図9 日本列島の累積地殻変動量
国土地理院公開の地殻変動補正パラメータを利用してアイサンテクノロジー社が図化
国土地理院は、セミ・ダイナミック補正実現のため、毎年の年度初めの4月1日に、地殻変動補正パラメータを公開します。全国に配置された約1,300点の電子基準点の地殻変動量を使って、約5km×5km格子点の地殻変動量が計算されます。この内挿には、TKY2JGDと同様に、クリギング法が使われています。地殻変動の期間は、元期からその年度の1月1日までです。1月1日の地殻変動量は、電子基準点の日々の座標を決めている「F3解(Final Solution)」によって推定されています。
図9は、地殻変動補正パラメータを使って、元期から2018.0までの累積地殻変動図です。西日本及び北海道は、元期1997.0から2018.0までの21年間の累積地殻変動です。2011年東北地方太平洋沖地震地域の1都19県は、元期2011.4から2018.0までの6.6年間の累積地殻変動です。
地図は、元期の位置で表示されています。2018.0における衛星測位結果は、図9に示す累積地殻変動量だけ位置のずれとなります。日本最西端では、1.5mのずれになります。東北の震源付近の余効変動の大きい地域では1m程度のずれになります。従いまして、dm級の位置の正確さを確保するためには、地殻変動補正が必要になります。
5.2 セミ・ダイナミック リダクション
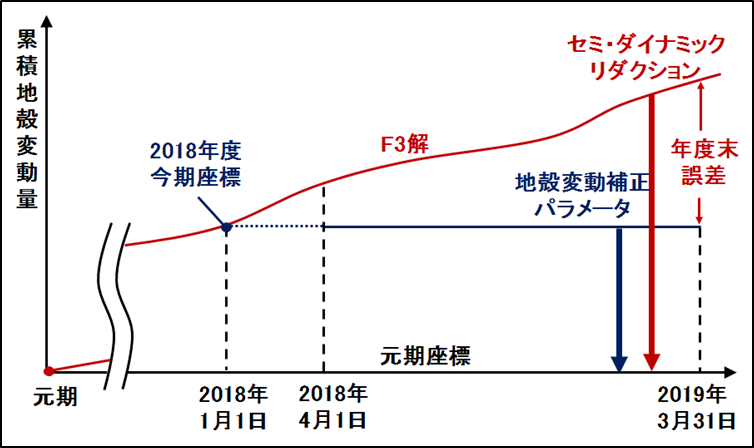
セミ・ダイナミック補正に使う地殻変動補正パラメータは、既に述べましたように、国土地理院が毎年4月1日に公開するものです。この補正に使う地殻変動補正パラメータは、日々の座標であるF3解から推定されたその年の1月1日の「今期(yy.0)」の座標が、その年度1年間を通じて使われます。年度末の3月の座標は、15か月前の座標であり、その期間のずれに相当する地殻変動誤差が生じます(図10参照)。誤差の平均的な大きさは、年間変動量に相当する数cm余と推定できます。
図10 セミ・ダイナミック リダクション
精密単独測位(PPP)のような座標観測は、その年度末誤差をまともに受けます。当社は、国土地理院が公表する日々の座標(F3解)を使って、地殻変動を受けたリアルタイムの観測値を元期に化成(リダクション)するcm級位置の正確さを保証する「セミ・ダイナミック リダクション」を開発しました。このシステムは第3期地理空間情報活用推進基本計画に基づくもので、用語は公的なものではありません。セミ・ダイナミック補正は、位置の相対測位に対する地殻変動量の微分量を補正するものです。それに対して、セミ・ダイナミック リダクションは、位置の絶対測位に対する地殻変動量の積分量の補正になります。
『第1回 その3 – 測量法に基づく測量の基準』へ
座標系講座 生活編
第1回 その3 – 測量法に基づく測量の基準
6. 震災復旧測量
1880年代に測量が開始された直後の1891(明治24)年に測量中の岐阜県濃尾地方で巨大地震が発生しました。この地震の規模は、マグニチュード8.0で、世界でも最大級の内陸直下型地震でした。地震に伴う地殻変動は、震災復旧測量として修正されてきました。
6.1 測量法第31条(測量成果の修正)
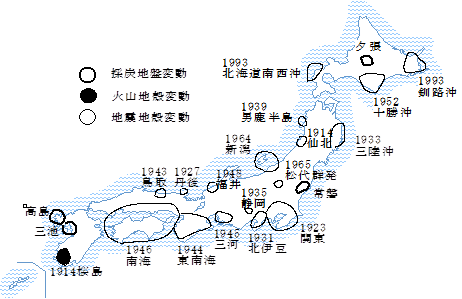
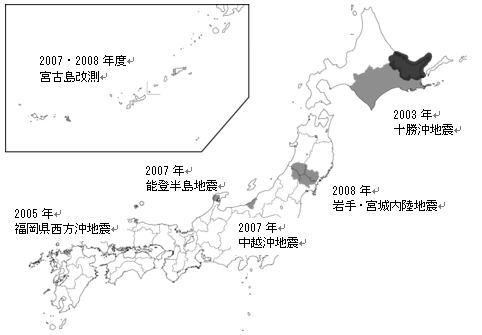
昭和24年の測量法第31条(測量成果の修正)は、“国土地理院の長は、地かく、地ぼう又は地物の変動その他の事由により基本測量の測量成果が現況に適合しなくなった場合においては、遅滞なく、その測量成果を修正しなければならない。”と定めています。図11は、濃尾地震後の日本測地系時代に発生した地震とその復旧測量地域です。火山活動地域及び採炭による地盤変動域も含まれています。
図11 地震・火山による改測・改算された地域及び地盤変動の大きい炭坑地域
6.2 PatchJGD座標補正
2002年度の日本測地系2000施行後、2003年に十勝沖地震(マグニチュード8.0)が発生しました。この地震は、震源が海部である海溝型であったため、陸地での地殻変動は、比較的一様なものでした。この地震による測量成果修正のため、地震前の座標を地震後の座標に補正するPatchJGD(参考文献3.飛田、2009)が開発されました。TKY2JGD座標変換プログラムと同様、三角点等の新旧座標差から1km×1kmの格子点上の座標補正量が計算され、これは「座標補正パラメータ」と呼ばれています。2003年十勝沖地震が発生した地域は、このPatchJGDにより測量法第31条に定める測量成果の修正が行われました(図12)。
この地震に伴う地殻変動は、北海道中央部において地殻変動がない不動地域と仮定して南半分の地域の地殻変動が計算されました。帯広地方では、1mに達しています。従いまして、この地震地域における日本測地系地図と衛星測位との整合は、次のような補正が必要になります。
- TKY2JGDによる日本測地系から日本測地系2000への座標変換:約450m
- PatchJGDによる2003年十勝沖地震の地殻変動補正:最大1m
- セミ・ダイナミック補正(又はセミ・ダイナミック リダクション):dm
図12 PatchJGDによる座標補正パラメータが公開されている地域
7. 2011年東北地方太平洋沖地震と日本測地系2011
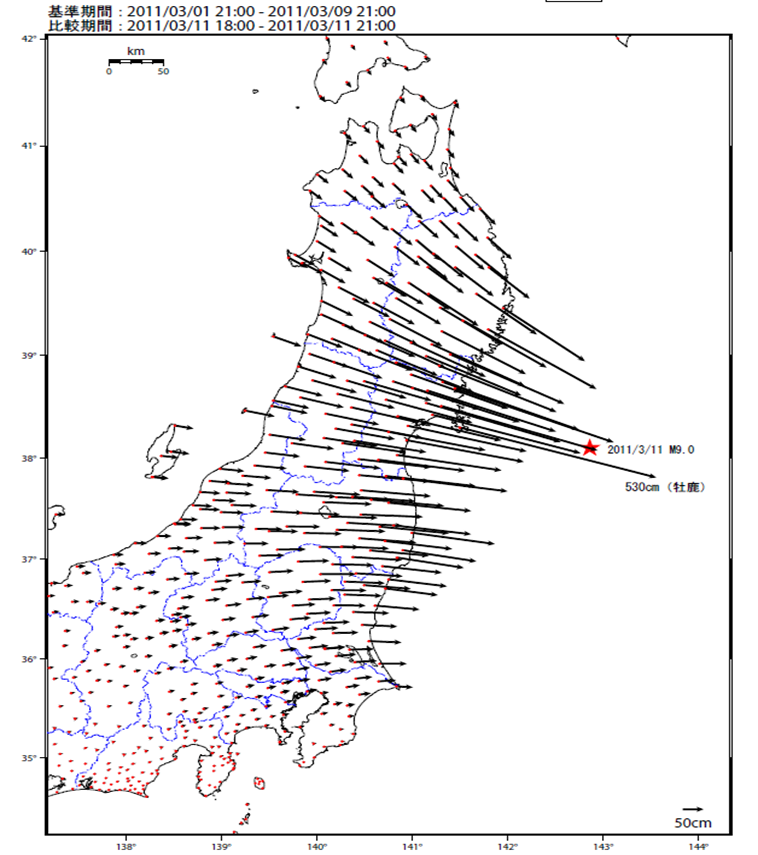
2011年3月11日の「2011年東北地方太平洋沖地震」は、広範囲に渡って大きな地殻変動を発生させました(図13)。地震発生後、東北、関東及び北陸地方等の1都19県の約4.4万点の測量成果が公表停止されました。水準点約1500点も併せてその成果が公表停止されました。公表停止された地域における約1846点が、364点の電子基準点を既知点として改測され、地震後の成果とされました。これらの地震後の成果約2200点の地殻変動量から地殻変動補正が計算され、PatchJGDにより、約4.1万点の三角点成果の修正が行われました。
この測量成果は、「日本測地系2011」とされました。日本測地系2011は、地震の影響を受けた地域だけでなく、日本の測量成果全体が日本測地系2011と名付けられました。
図13 2011年東北地方太平洋沖地震に伴う地殻変動
国土地理院(http://www.gsi.go.jp/common/000059672.pdf)による
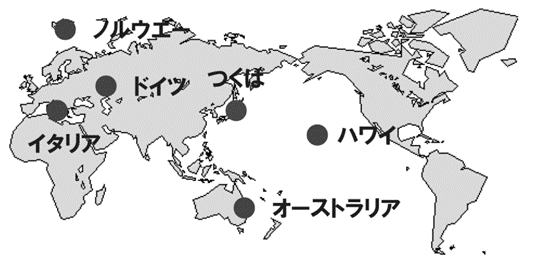
2003年の十勝沖地震等これまでの地震の地殻変動は、日本国内に不動点が仮定され、その不動点を既知点として改測により、地震後の位置が計算されました。2011年東北地方太平洋沖地震の場合、地殻変動規模が大きく、図14に示すように、国外に不動点が設けられました。ITRF2008観測網のうち日本周辺の5か所のVLBI観測点を選び、つくばVLBI観測点の座標を決定しました。つくばVLBI観測点の座標は、ITRF2008(元期2011.4)と決められました。
図14 周囲5点を不動点としてつくばVLBI観測点の地殻変動後の座標を決定
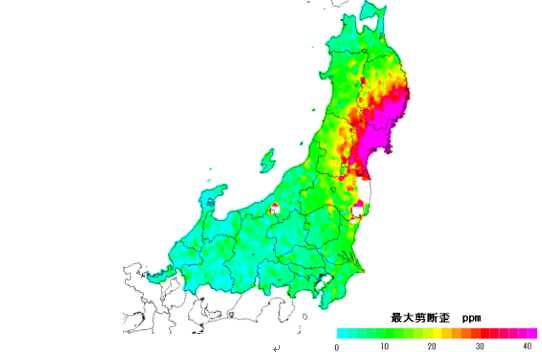
図15は、座標補正パラメータから計算した最大剪断歪です。震源地に近い地域において歪みが大きく、こうした地域において、PatchJGDによる座標補正は、慎重に検討すべきです。
図15 PatchJGDによる座標補正誤差の推定
国土地理院公開の座標補正パラメータを利用してアイサンテクノロジー社が図化
図15に示す地震域において、日本測地系2000に基づく地図は、衛星測位結果と最大5mの座標補正量相当のずれを生じます。そのずれを無くすには、PatchJGDによる座標補正を行い、日本測地系2011の座標の地図で扱わなければなりません。
『第1回 その4 – 測量法に基づく測量の基準』へ
座標系講座 生活編
第2回 地理空間情報活用推進基本法等衛星測位関連法
衛星測位及び地上の位置に関する法律は、先述の測量法以外に、次のものがあります。地理空間情報活用推進基本法、国土調査法及び不動産登記法です。以下、これらの法律と衛星測位との関係を考察します。
1. 地理空間情報活用推進基本法(平成19年5月30日法律第63号)
本法律は、地理空間情報の活用の推進に関する施策を総合的かつ計画的に推進すること及び我が国独自の準天頂衛星による衛星測位システムの推進が目的です。本法律第二条は、次にように、(X,Y,Z,t)の4次元の位置情報を定義しています。
この法律において「地理空間情報」とは、第一号の情報又は同号及び第二号の情報からなる情報をいう。
| 一 | 空間上の特定の地点又は区域の位置を示す情報(当該情報に係る時点に関する情報を含む。以下「位置情報」という。) |
| 二 | 前号の情報に関連付けられた情報 |
平成20年4月の「第1次地理空間情報活用推進基本計画」は、“測量の基準点は、基盤地図情報の骨格をなすものであるが、日本列島では地殻変動による位置精度の劣化が懸念される。このため、国土地理院は、基準点測量を計画的に実施するとともに、セミ・ダイナミック補正(基準点測量の結果から地殻変動の影響を取り除く方法)を導入して、国家基準点体系の維持、確かな位置情報の提供を図る。” と定めました。この決定に基づいて、国土地理院は、かねてから検討していたセミ・ダイナミック補正を2010年に導入しました。
【注】測量法は、位置の時間変化に関しては、同法第31条に定められた(測量成果の修正)です。測量法には、定常的な地殻変動に対応する法律的根拠は定められてなく、定常的な地殻変動に関する法律的根拠は、地理空間情報活用推進基本法に委ねられることになります。
地理空間情報活用推進基本計画は、平成19年に制定された地理空間情報活用推進基本法に基づき、翌年4月には第1期の、平成24年3月には第2期の地理空間情報活用推進基本計画(以下「基本計画」という。)を策定し、平成29年3月には第3期の基本計画を策定してきています。こうした基本計画の中で平成30年度における4機体制の運用及び平成35年度を目途とした7機体制の確立が決定されているところです。
2. 国土調査法(昭和26年法律第180号)
国土調査法は、国土の開発及び保全並びにその利用の高度化に資するとともに、あわせて地籍の明確化を図るため、国土の実態を科学的且つ総合的に調査することを目的とするものです(第1条)。
1951(昭和26)年に開始された調査は、65年を経過した2016(平成28)年度末において、平均52%の進捗率です。特に、都市部の進捗率は24%及び林地は45%と調査が進んでいません。地籍調査事業の遅れの最大の原因は、日本における測量・地図事業が軍用目的に行われたためでしょう。本格的な地籍調査は、昭和26年の国土調査法成立から始まりました。また、各1都2府47県の地籍調査担当部署は、6割が農林部などで担当し、この地籍調査事業が農業政策として実施されていることも、都市部での進行を妨げているのでしょう。
地籍調査の成果は、測量法第11条の測量の基準に基づいて作成された地籍図です。準天頂衛星は、高層ビル地帯の都市部や林地での活躍が期待でき、地籍調査へのその活用が有力です。また、地籍測量は、基準点測量と細部測量で構成されていますが、精密単独測位が本格化すれば、基準点測量は省略でき、細部測量のみで成果が得られます。
3. 不動産登記法(平成16年法律第123号)
不動産登記法は、“不動産の表示及び不動産に関する権利を公示するための登記に関する制度について定めることにより、国民の権利の保全を図り、もって取引の安全と円滑に資することを目的とする。”ことを目的としています。
不動産登記法に基づく地図は、不動産登記法「第14条第1項地図」及び「同第4項地図」並びに不動産登記令第2条に定められた「地積測量図」があります。
3.1 不動産登記法第14条地図
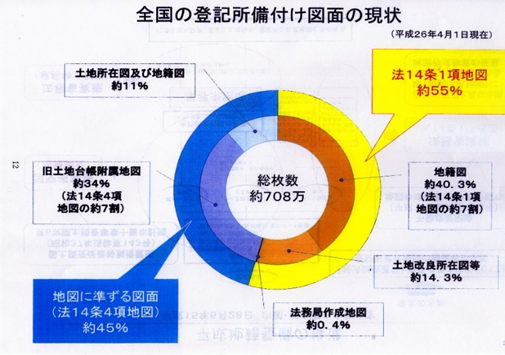
地籍調査の成果は、地籍図として、実施地方自治体及び法務省の登記所に保管されています(図 1)。地籍図は、法務省に送られ、不動産登記法第14条第1項地図として備え付けられています。その数は、登記所備付図面708万枚の約55%になります。図1に示す地図に準ずる図面(法第14条第4項地図、約45%)は、測量法の測量の基準に基づく位置が決められていない位置の不正確な地図です。
図1 全国の登記所備え付け図面
平成30年地積問題研究会第21回定期研究会配布資料
3.2 地積測量図
不動産登記令(平成16年12月1日政令第379号)第2条に定められた“一筆の土地の地積に関する測量の結果を明らかにする図面”である地積測量図は、不動産登記規則(平成17年法務省令第18号)第77条によって、その作成が定められています。不動産登記規則第10条第3項は、測量法に基づく「基本三角点等」に基づいて地積測量図の座標化を定めています。基本三角点等が存在しない地域において、準天頂衛星測位に基づいた座標観測により、地積測量図の座標化が容易になります。ちなみに、地籍調査における年間の認証筆数は約70万に対して、地積測量図の扱う認証筆数は約200万です。衛星測位の活用による地積測量図の座標化は、遅れている地籍調査への支援にもなるでしょう。
『第3回 土地の高さ』へ
座標系講座 生活編
第1回 その4 – 測量法に基づく測量の基準
8. フレーム境界における座標の不整合
日本全国に約1,300点の電子基準点が配置され、これらの電子基準点の座標は、「ITRF2005」に基づく「IGS05」と結合し、リアルタイムの位置が正確に決められています。一方、日本の位置は、測量法第11条によって定められていますから、日々得られる電子基準点の位置は、測量法上の位置ではありません。測量法的には、日本経緯度原点を出発点として、日本全国の位置が決められます。
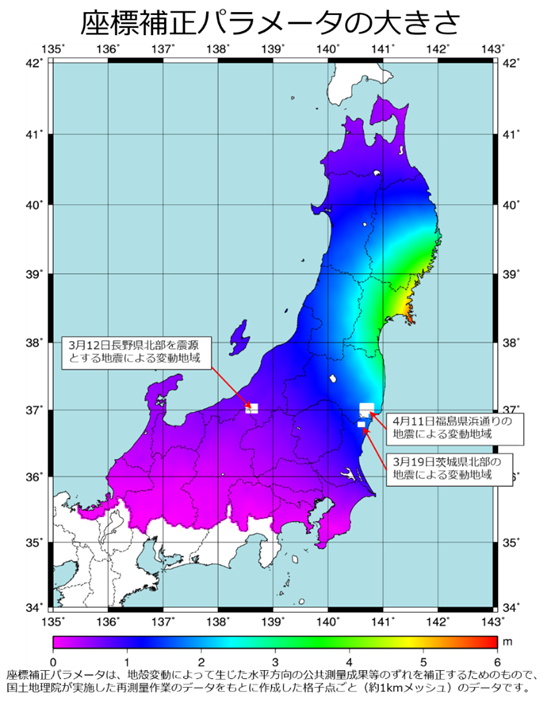
図16 座標補正量
色塗り地域ITRF2008(元期2011.4)及び白色地域ITRF94(元期1997.0)
国土地理院<http://www.gsi.go.jp/common/000109975.png>より
図16は、2011年東北地方太平洋沖地震地域における座標補正量です。色塗り地域は、ITRF2008(元期2011.4)で地震後の座標へと補正がされた地域です。それに対して白色地域及び北海道は、ITRF94(元期1997.0)で、座標は地震前のままです。日本の座標系は、測量法的には二つのフレームで構成されています。そのため、フレームの境界では座標の不整合が生じます。その座標の不整合を調整するため、富山県、石川県及び福井県の北陸3県並びに岐阜県の4県がその緩衝地域となりました。ただし、本州―北海道境界は、津軽海峡で隔たれていますから、フレームの食い違いは、直接影響が生じません。以下、その考察を行います。
図17は、国土地理院公開による地震直後の「Semidyna2011.par」を使ってアイサンテクノロジー社が図化したものです。2011年東北地方太平洋沖地震の1都19県の位置は、元期2011.4です。一方、Semidyna2011.parの基準日は、元期と同じ2011.4となっています。従いまして、ITRF2008(元期2011.4)地域の地殻変動補正量は、ITRF2008座標及びパラメータ計算に用いたF3解の座標に誤差が無いとすれば、零になるはずです。
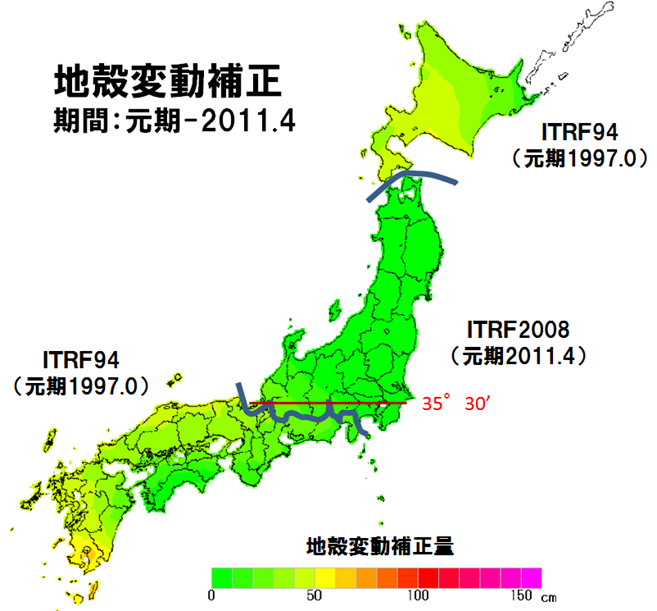
図17 地殻変動量図
国土地理院公開「Semidyna2011.par」を利用してアイサンテクノロジー社が図化
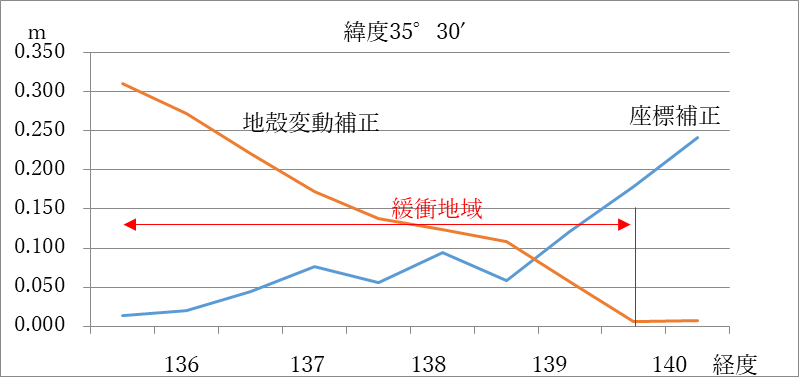
図18は、緯度35°30’ に沿ったJGD2000(元期1997.0)からJGD2011(元期2011.4)への座標補正及びJGD2011への地殻変動補正量を示したものです。ITRF2008(元期2011.4)の地域における地殻変動補正量は 、本来零のはずです。ITRF94(元期1997.0)と整合させるため、フレーム境界においてITRF94(元期1997.0)による地殻変動量と整合させています。一方、座標補正は、境界付近の補正量を零に近くして、フレーム境界での座標の不整合を生じないようにして(参考文献4. 檜山他,2011)図16に示す座標補正を行っています。
図18 緯度35°30’に沿った座標補正及び地殻変動補正
2011年3月14日の座標修正の当初計画は、長野県及び新潟県がフレームの境界でした。しかし、境界での不整合が大きく、5月31日に、北陸・岐阜4県がフレーム境界の不整合の緩衝地域ITRF2008に組み込まれました。この地域は、ITRF2008で元期及び今期ともに2011.4であるにも関わらず、地殻変動補正量は、零でなく緩衝のため地殻変動補正量(図18)が与えられています。
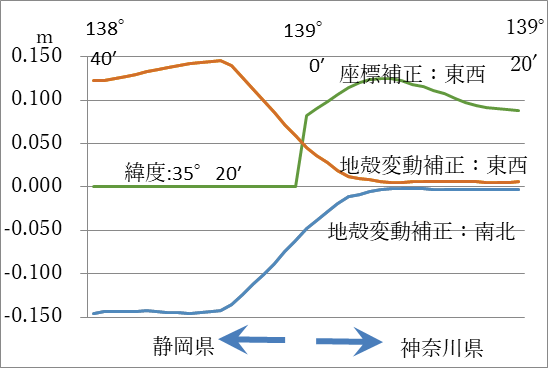
図19 緯度35°20′に沿ったフレーム境界:静岡県(元期1997.0)-神奈川県(元期2011.4)間の
地殻変動補正及び座標補正(東西)
静岡県と神奈川県のフレーム境界の場合、北陸・岐阜4県のような緩衝地帯がなく、図19に示すように、地殻変動補正の緩衝地域を静岡県側に設定しています。座標補正は、ITRF94のフレームである静岡県を零として、神奈川県側の座標補正量が示されています。
以上のまとめとして、次のことが言えます。
- 日本列島の測量法上の位置は、ITRF94(元期1997.0)とITRF2008(元期2011.4)の二つのフレームを使っている。
- フレームの境界である本州と北海道の境界は、津軽海峡で陸続きではない。そのため、陸地上での座標の不整合は、問題にならない。
- 東日本と西日本のフレーム境界は、北陸・岐阜4県の座標の緩衝地域を設けることで、座標の食い違いをグラデーション化している。
- 北陸・岐阜4県の三角点及び電子基準点座標は、ITRF2008(元期2011.4)である。地殻変動補正(基準日2011.4)は、零のはずであるが、緩衝処理分だけ零から離れる。
- そのため、北陸・岐阜4県において得られた精密単独測位の座標は、座標緩衝処理分を考慮した地殻変動補正量により、測量法上の位置にする。
8. 地図の品質
「公共測量作業規程の準則」第80条数値地形図データの位置精度及び地図情報レベルは、表2を標準とすることを定めています。誤差の許容範囲を2σとすれば、衛星測位結果と地図は、下表の2倍程度の位置のずれを生じることになります。ただし、地図の品質評価が定かでない民間事業により作成された地図の品質は不明です。
表 2 数値地形図データの位置精度及び地図情報レベル
10. まとめ
準天頂衛星4機体制は、2018年度中に運用が開始され、日本における衛星測位の活用が一段と高まります。既に述べてきましたように、正確な衛星測位結果が、私達国民生活に貢献するには、地上での正確な地図等の位置情報と対でなければなりません。その地上の位置情報は、測量法第11条測量の基準が大きな役割をしています。以下にその内容を列挙します。
- 明治時代から2001年度までに作成された位置は、古い技術である天文測量及び三角測量によるもので、現在の衛星測位の位置と約400m余りずれています(図3)。これらの古い地図は、国土地理院が提供するTKY2JGD座標変換プログラムと座標変換パラメータに基づいて、衛星測位成果である世界測地系(日本測地系2000)に座標変換しなければなりません。
- 2011年東北地方太平洋沖地震により大きな地殻変動を受けた地域(図13)においては、PatchJGD座標補正プログラムと座標補正パラメータに基づいて、地震後の日本測地系2011へ座標補正しなければなりません。最大の補正量は、5m程度(図16)です。
- 日本列島の定常的地殻変動は、年平均数cmと大きく(図9)、元期の位置で作成された地図との整合は、地殻変動補正パラメータ又はセミ・ダイナミック リダクションにより、元期の位置に還元しなければなりません。平均的補正量はdm単位ですが、沖縄及び東北の余効変動域では最大の補正量は1mを超える地域があります。
- 2003年十勝沖地震等による地殻変動は(図12)、PatchJGD座標補正パラメータにより地殻変動後の位置に補正しなければなりません。最大の補正量は1m程度です。
- 現存の地図は、①日本測地系から世界測地系への座標変換誤差②地図作成誤差などの地図作成誤差を有しています(表2)。誤差の大きさはdm単位です。
『第2回 地理空間情報活用推進基本法等衛星測位関連法』へ
参考文献
- 宮原伐折羅(2015):地球規模の測地基準座標系に関する国連総会決議と国土地理院の貢献,国土地理院時報 No.127
- 飛田幹男(2002):世界測地系移行のための座標変換ソフトウエア“TKY2JGD”,国土地理院時報 No.97.
- 飛田幹男(2009): 地震時地殻変動に伴う座標値の変化を補正するソフトウエア”PatchJGD”,測地学会誌,第55巻, 355-367頁.
- 檜山洋平・山際敦史・川原敏雄・岩田昭雄・福﨑順洋・東海林靖・佐藤雄大・湯通堂 亨・佐々木利行・重松宏実・山尾裕美・犬飼孝明・大滝三夫・小門研亮・栗原 忍・木村勲・堤 隆司(2011):平成23 年(2011年)東北地方太平洋沖地震に伴う基準点測量成果の改定,国土地理院時報 No.122.
< http://www.gsi.go.jp/common/000064457.pdf >
座標系講座 生活編
第4回 ISO(JIS)に基づく地球上の位置表示
2008年3月31日、国土地理院は57年ぶりに公共測量作業規程の準則を改正しました。この改正の大きな特徴は、ISOに基づく「地理情報標準プロファイル:JPGIS(Japan Profile for Geographic Information Standards)」を導入したことです。すなわち、日本の測量関係に国際標準が導入されたことであり、画期的なことです。
本章は、国土地理院ウェブサイトに示された下記文献等に基づいて地球上の位置表示を考察します。これらの文献は、基本的にISOに基づくもので、文献の引用は□で囲ってあります。
- 地理情報標準推進委員会 国土地理院、地理情報標準第2版(JSGI2.0)解説、平成14年3月
- 同上付録地理情報標準専門用語集Ver.2(以下、用語集という。)
- 空間データ製品仕様書作成マニュアルJPGIS 版、Ver.1.0、平成17 年3 月
- 地理空間データ製品仕様書作成マニュアル 平成26年4月(以下、製品仕様書作成マニュアル(平成26年)という。)
- JIS X 7111(2014)
なお、本章の多くは、(参考文献1.中根・横井,2015)における第2章を転写したものです。
1. 座標と座標系
下記は、用語集による「座標」及び「座標系」の定義です。
| 座標の定義 | n 次元空間内の点の位置を示すためのn 個の数値の列の中の1つの数。 |
| 備考 | 座標参照系の中では,数は単位を付与することによって,意味をなす。 |
| 座標系の定義 | 点にどのように座標を割り当てるかを規定する(数学的)規則の集合。 |
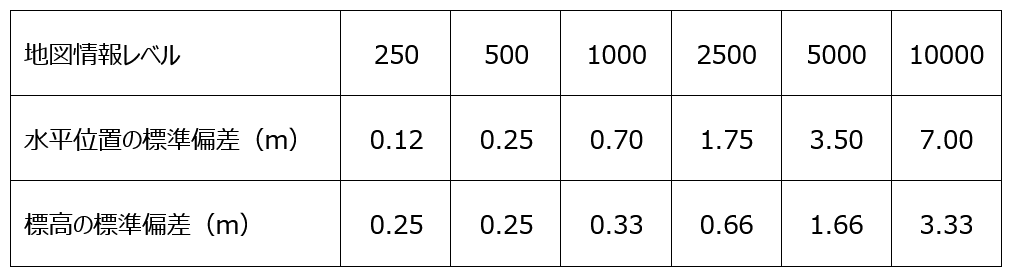
図1は、「平面直角座標系(n=2)」及び「3次元直交座標系(n=3)」におけるそれぞれのP点の座標(2.0, 2.5)及び(1.3, 1.9, 2.3)を示したものです。
図1 座標系(左:平面直角座標系、右:3次元直交座標系)と座標
次に測量で使う座標系の定義を考察します。
1.1 直交座標系
下記は、用語集による「直交座標系(Cartesian coordinate system)」の定義です。
| 定義 | 点の位置をN本の相互に直交する軸に関して与える座標系。 |
| 備考 | この規格の目的では,Nは1,2又は3である。 |
| 筆者注: | 国土交通省告示(平成14年国土交通省告示第9号)による「平面直角座標系」及び国土交通省告示(平成14年国土交通省告示第185号)「地心直交座標系」は、この定義に合致します。 |
1.2 楕円体座標系又は測地座標系
下記は、用語集による「楕円体座標系(ellipsoidal coordinate system, geodetic coordinate system)」又は「測地座標系(geodetic coordinate system)」の定義です。
| 定義 | 位置が測地経緯度及び(三次元の場合は)楕円体高によって指定される座標系。 |
| 楕円体高 | h (ellipsoidal height) |
| 楕円体高の定義 | 楕円体からある地点までの垂線に沿って測られる楕円体からその地点までの距離,楕円体の上側又は外側に向かう場合は正。 |
| 備考 | 三次元測地座標系の一部として使われるだけでそれ自体では使われない。 |
1.3 鉛直座標系
用語集は、「鉛直座標系(vertical coordinate system)」及び標高の定義を示していません。JIS X 7111(2014)は、標高(orthometric height)又は正規高(normal height)を表示する1次元の座標系として鉛直座標系を定義しています。ここでは、ISOの定義“gravity related height”が“標高”と日本語化されています。従って、JISでは、現代測地学で重要な役割をなす正規高の存在が薄められています。
2. 原子
下記は、用語集による「原子(datum)」の定義と解説です。
| 定義 | 別のパラメタの計算のために参照したり基礎として使われるパラメタ又はパラメタの集合。 |
| 備考 | 1)原子は地球に関係する座標系の軸の原点の位置,縮尺,及び向きを定義する。2)原子は測地原子,鉛直原子,又は施工基準原子であっても良い。 |
| コメント | dataは,科学的・学術的な著述においては,ほぼ決まって複数扱いとなる。その他の場合は,単数扱いとも複数扱いともなる。単数形の datum が「1つの情報」の意味で用いられるのは,いずれの場合でもまれである。測量学や土木工学では datum が専門語として使われるため,複数形は datums となる(小学館ランダムハウス英語辞典(Windows版)Version 1.1,1998)。Datumに対して「基準」と訳すべしとの意見があるが,測地学では古くから「原子」といっており,「基準」は準拠楕円体そのものをあらわすときに使うreferenceの訳語である。 |
2.1 測地原子
下記は、用語集による「測地原子(geodetic datum)」の定義です。
| 定義 | 座標系と地球の間の関連付けを記述する原子。 |
| 備考 | 多くの場合,測地原子は楕円体の定義を含む 。 |
JIS X 7111(2014)は、次のように定義していて、用語集の定義と若干異なります。
定義 :二次元又は三次元座標系と地球との関係を記述する原子。
測地原子の例
上記の定義に従えば、測地原子は、経緯度原点の緯度φ、経度λ及び楕円体高h並びに長半径及び扁平率です。経緯度原点の地心直交座標(X,Y,Z)は、楕円体の形状の原子である長半径及び扁平率の2量を与えれば、(φ, λ,h)と等価な測地原子になります。
日本の測地原子
国土地理院は、“測地原子は、測量法及び同施行令に拠る。”としています(質問に対する回答)。この基準によれば、日本の測地原子は、次のようになります。
- 日本測地系:平成14年3月31日時点の測量法第11 条に定める回転楕円体の長半径及び扁平率並びに測量法施行令第2条に定める日本経緯度原点の地点及び原点数値により規定される測地原子。
- 日本測地系2000:平成14年4月1日時点の測量法施行令第2条に定める日本経緯度原点の地点及び原点数値並びに同第2条の2に定める回転楕円体の長半径及び扁平率によって規定される測地原子。
- 日本測地系2011:平成23年10月21日時点の測量法施行令第2条に定める日本経緯度原点の地点及び原点数値並びに同第3条に定める回転楕円体の長半径及び扁平率によって規定される測地原子。
以上のように、日本の測地原子は、日本測地系(Tokyo Datum)、日本測地系2000 (JGD2000)及び日本測地系2011(JGD2011)の3種類です。いずれも楕円体原子2量並びに位置の原子である日本経緯度原点の緯度、経度及び方位角であって、楕円体高は含まれていません。
2.2 鉛直原子
下記は、用語集による「鉛直原子(vertical datum)」の定義です。
| 定義 | 重力に関係する標高と地球の関係を記述するパラメタの集合。 |
| 備考 | ほとんどの場合,鉛直原子は海水面と関係付けられることになる。楕円体高はある測地原子に準拠した三次元楕円体座標系に関連付けられたものとして扱われる。鉛直原子は水深測定用の原子(水路測量目的で用いられる)を含む。この場合,高さは負の高さ又は深さとしてもよい。 |
日本の鉛直原子
日本における具体的な鉛直原子は、“測量法施行令第2条に定める日本水準原点の地点及び原点数値によって規定される鉛直原子”です。鉛直原子の別名として“東京湾平均海面”及び鉛直原子の識別子として “TP”を適用しています。明治以来約130年間の日本の鉛直原子は、水準原点の標高が2回改正されているにもかかわらず、東京湾平均海面(TP)のみで表示されています。
3. 座標参照系
下記は、用語集による「座標参照系(coordinate reference system)」の定義です。
| 定義 | 原子により実世界に関連づけられた座標系。 |
| 備考 |
採用した座標で利用するための原子,座標系,及び換算(地図投影法のような)の定義を含む。 |
JIS X 7111(2014)は、座標参照系を「測地座標参照系」と「鉛直座標参照系」に分けています。
3.1 測地座標参照系
「測地座標参照系(geodetic coordinate reference system)」は、測地原子に基づく座標参照系です。測地座標参照系には、次のようなものがあります。
三角測量の測地座標参照系
三角測量時代の測地座標参照系は、2次元表示です。
- 測地原子(経緯度原点の緯度、経度及び方位角)により地球上の位置を表示する楕円体座標系(緯度、経度)
- 測地原子(経緯度原点の緯度、経度及び方位角)により地球上の位置を表示する平面直角座標系(系:X座標、Y座標)
衛星測位の測地座標参照系
衛星測位時代の測地座標参照系には次のものがあります。
- 測地原子(経緯度原点の緯度、経度及び楕円体高並びに楕円体の形状を表す原子)により地球上の位置を表示する楕円体座標系(緯度,経度,楕円体高)
- 測地原子(経緯度原点のX,Y,Z)により地球上の位置を表示する地心直交座標系(X,Y,Z)。楕円体の形状を表す原子が与えられれば、上記1.の座標参照系と等価である。
- 測地原子(経緯度原点の緯度及び経度)により地球上の位置を表示する平面直角座標系(系:X座標,Y座標)
日本における座標参照系
製品仕様書作成マニュアル(平成26年)は、“JPGISに準拠する製品仕様書では,『附属書2(規定)座標参照系』に従い,地理空間データ製品の座標参照系として『JIS X 7115附属書2(規定)日本における座標参照系の表記』に定められた表記規則に基づく識別子を記述する。” として、座標参照系の記述方法を次のように定めています。
座標参照系(識別子)= 原子 / 座標系
【注】原子と座標系を区別する「 / 」の両側は半角スペースを入れる。
具体例として、次が示されています。
| 測地原子 | 別名:日本測地系2011 | 識別子:JGD2011 |
| 測地座標系 | 別名:緯度,経度 | 識別子:B,L |
| 測地座標参照系 | 別名:日本測地系2011 / (緯度,経度) | 識別子:JGD2011 / (B,L) |
| 測地原子 | 別名:日本測地系2011 | 識別子:JGD2011 |
| 平面直角座標系 | 別名:平面直角座標系Ⅶ(X座標,Y座標) | 識別子:7(X,Y) |
| 測地座標参照系 | 別名:日本測地系2011 / 平面直角座標系Ⅶ(X座標,Y座標) | 識別子:JGD2011 / 7(X,Y) |
3.2 鉛直座標参照系
鉛直座標参照系(vertical coordinate reference system)は、鉛直原子に基づく座標参照系です。鉛直座標参照系には、次のものがあります。
| 鉛直原子 | 別名:東京湾平均海面 | 識別子:TP |
| 鉛直座標系 | 別名:標高 | 識別子:H |
| 鉛直座標参照系 | 別名:東京湾平均海面 / 標高 | 識別子:TP / H |
3.3 複合座標参照系
下記は、用語集による複合座標参照系(compound coordinate reference system)の定義です。
| 定義 | 独立した二つの座標参照系による空間位置の記述。 |
| 利用例 | 二又は三次元の幾何的な座標系を基礎とする座標参照系及び重力に関係する標高系に基づくもう一つの座標参照系。 |
下記は、測地座標参照系と鉛直座標参照系による複合座標参照系です。
| 別名 | 日本測地系2011, 東京湾平均海面 / (緯度,経度), 標高 |
| 識別子 | JGD2011, TP / (B,L), H |
| 別名 | 日本測地系2011, 東京湾平均海面 / 平面直角座標系(X座標,Y座標) , 標高 |
| 識別子 | JGD2011, TP / 7(X,Y), H |
| 【注】 | 原子1と原子2の区切りは「,」の後に半角スペースを入れる。同様に、異なった座標系の区切りとして「,」の後に半角スペースを入れる。 |
図2 複合座標参照系
3.4 地心直交座標参照系の例
JIS X 7111(2014)は、三次元測地座標参照系(地心直交X,Y,Z)を示しています。それにならえば、次の座標参照系をつくることができます。
別名: 日本測地系2011 / 地心直交座標系(X座標,Y座標,Z座標)
識別子:JGD2011 / (X,Y,Z)
地心直交座標系の日本経緯度原点の測地原子は、平成23年10月21日国土交通省告示第1063号に定められています。
4. 座標演算
下記は、用語集による「座標演算(coordinate operation)」の定義です。
| 定義 | ある座標参照系から他の座標参照系への一対一の関係に基づく座標の変更。 |
| 備考 | 座標変換及び座標換算の上位型。 |
4.1 座標変換
下記は、用語集による「座標変換(coordinate transformation)」の定義です。
| 定義 | 異なる原子に基づくある座標参照系から他の座標参照系への一対一の関係による座標の変更。 |
| 備考 | 座標変換は両座標参照系で共有する点の集合により経験的に導くことができるパラメタを使用する。 |
| コメント | この定義は測地学の定義である。 |
| 筆者注: | 日本における座標変換の代表例は、①日本測地系と日本測地系2000 ②ITRF94とITRF2008です。 |
4.2 座標換算
下記は、用語集による「座標換算(coordinate conversion)」の定義です。
| 定義 | 同一原子上におけるある座標系から他の座標系への一対一の関係に基づく座標の変更[地理情報標準第2版-座標による空間参照] |
| 利用例 | 測地座標系と直交座標系間の換算,測地座標と投影座標間の換算,若しくはラジアンと度のような単位の換算。 |
| 備考 | 換算には定数パラメタを使用する。 |
| 筆者注: | 座標換算の代表例は、3次元の場合、楕円体座標参照系(B,L,h)と地心直交座標参照系(X,Y,Z)です。2次元の場合、楕円体座標参照系(B,L)と平面直角座標系(X,Y)です。 |
4.3 座標変換と座標換算の区別
古い教科書類は、座標変換と座標換算の定義が明確でなく、両者はひっくるめて座標変換の用語でまかなわれることが多く見られました。その影響と思われますが、準則の計算式集に記載された平面直角座標系と楕円体座標系との距離及び方向角の化成(reduction)が変換(transformation)とされています。
『第5回 まとめ』へ
参考文献
1.中根勝見、横井貴史(2015):衛星測位時代における測地学・ISO・測量法に基づく地球上の位置を表す理論とその仕組み、アイサンテクノロジー株式会社.
座標系講座 生活編
第3回 土地の高さ
測量法上の土地の高さは、測量法第11条に基づくもので、日本水準原点を出発点に水準測量により水準点の高さが決められます。この高さは、定常的地殻変動の影響を考慮しないスタティック標高系によるものです。また、衛星測位による楕円体高の測定結果からジオイド高を減じて得られる高さがあります。この高さは、セミ・ダイナミック測地系の扱いで、地殻変動の影響が考慮されています。当然、これらの2種類の高さは、一致しません。なお、測量で使われる高さは「標高」と呼ばれています。また、ISOでは、「重力関連高(gravity related height)」と呼ばれています。
1. 水準測量により得られる標高
地殻変動の大きい日本列島では、明治以来9回余り繰り返し水準測量が行われてきました。水準測量路線は、連載第1回の図5に示したところです。こうした改測成果に基づいて、1969年(北海道は1972年)に水準点標高成果が更新されました。その後、世界測地系導入時に「2000年度平均成果」として更新されました。
2011年東北地方太平洋沖地震に伴って、水準点約2000点が改測されその成果が修正されました。この地域は、余効変動が大きく、2017年及び2018年に再度改測が行われ水準点成果の修正が行われました。
2. 衛星測位により得られる標高
衛星測位から得られた楕円体高からジオイド高を差し引いて、標高を求めることができます。ジオイド高は、国土地理院によって公開されています(図1)。
図1「日本のジオイド2011」(Ver.2)
等ジオイド高線間は1m,適用:赤枠内「日本のジオイド2011」(Ver.2)で更新した地域,
その他の地域「日本のジオイド2011」(Ver.1)
国土地理院(http://www.gsi.go.jp/common/000196728.pdf)
衛星測位から求める楕円体高からジオイド高を減じて得られる標高は、地殻変動の影響を考慮したセミ・ダイナミック測地系によるものです。図2は、国土地理院が公開した地殻変動補正パラメータを使って、元期から2018.0までの累積上下変動を表したものです。2011年東北地方太平洋沖地震時に1m程度沈下した石巻付近の余効変動は、その後最大で40cm程度隆起しています。
図2 元期から2018.0までの累積上下変動量
国土地理院公開の地殻変動補正パラメータを利用してアイサンテクノロジー社が図化
この地域の住民は、景観上、防潮堤の高さを可能な限り低いものを望んでいました。そのためには、地震後の余効変動により隆起した高さだけ低くできます。測量法上の高さを決める水準点の高さを使った場合、隆起分は考慮されません。そんなこともあり、国土地理院は、再度水準測量を実施し、2017年2月に標高を決め、この標高により防潮堤の高さが決められました。ちなみに、隆起量は22cmになり、当初計画より22cm低い防潮堤建設が可能になりました。
3. 3種類の標高の選択
以上述べましたように、標高には2種類があります。水準測量から得られる標高は、地殻変動の影響は考慮されていない「スタティック標高系」です。一方、衛星測位の楕円体高は元期の標高であり、「セミ・ダイナミック標高系」になります。ただし、電子基準点の標高が水準測量によって決められ、ジオイド高を加えた楕円体高を使ってGNSS水準測量によって得られた標高は、スタティック標高系になります。更に、人間生活で必要な高さは、現時点の水面の高さに対応した値で、「ダイナミック標高系」によるものです。現時点の標高は、衛星測位により得られた観測時の標高からジオイド高を減じた値を使います。又は、東北地方のように、水準測量による成果の更新を行うことです。後者の場合、非常に手間がかかるので、衛星測位によるダイナミック標高系によるのが便利で、衛星測位の活用の場になります。
『第4回 ISO(JIS)に基づく地球上の位置表示』へ
実験結果レポート
CLASの評価(静止測位:2020.02版)
2020年03月04日
準天頂衛星の正式サービスが始まり既に1年以上経ち、多様な分野で実証実験が行われてきましたが、その多くは移動体による実証実験となっています。
そこで、今回は準天頂衛星のセンチメータ級測位補強サービス(CLAS)による高精度測位の可能性を評価するため、静止測位による実証実験を実施していました。
PDFダウンロードはこちらから
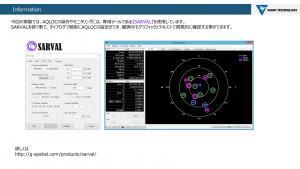
*今回の実験で利用した「GNSS-Explorer」,「SARVAL」についてはこちらで紹介しています。
誤差論と最小二乗法
第8回 線形モデル – その2
2020年03月17日
前回は基本の線形モデルを取り上げ、最小二乗法により未知パラメータを推定しました。今回は、もう一つの推定法である最尤法で未知パラメータを求めてみます。次に線形モデルを少し一般化したものを考えます。具体的には、![]() の場合です。各観測値の分散が異なる場合や相関を持つ場合に相当します。
の場合です。各観測値の分散が異なる場合や相関を持つ場合に相当します。
1. 最尤(推定)法
最小二乗法は線形モデルにおける基本的な方法ですが、様々なデータの中には線形モデルで記述するには不適切なものもあります。そのような場合に一般に用いられる方法が最尤法です。
最尤法は第6回に紹介しました。尤度関数を最大にする推定値を求める方法です。尤度関数とは観測値の確率密度関数において観測値は観測された値に固定し、パラメータを変数とみなしたものです。ここでは最尤法を正規分布の線形モデルに用いてみましょう。
線形モデル
![]()
において、観測値の分布を(n次元の)正規分布(付録B参照)
![]() の最尤推定値は上式の第3項を最大にするものですから残差二乗和
の最尤推定値は上式の第3項を最大にするものですから残差二乗和![]() を最小にするもの、つまり最小二乗法と同じになります。
を最小にするもの、つまり最小二乗法と同じになります。
最尤法は様々な分布を持つデータに用いることができる一般的な方法ですが、定義からもわかるように観測値の分布関数を仮定する必要があります。最小二乗法では特に分布関数の形に仮定はなく、分散(あるいは重み)のみが仮定されます。
2. 一般の最小二乗法
線形モデルにおいて各観測値の分散が必ずしも同じでない場合を考えます。すると、![]() を測定データ、
を測定データ、![]() を既知の計画行列、
を既知の計画行列、![]() を未知パラメータ、
を未知パラメータ、![]() をランダム誤差とするとモデルは
をランダム誤差とするとモデルは
と書けます。ここで、![]() は既知の正定値行列、
は既知の正定値行列、![]() は一般には未知とします。式
は一般には未知とします。式![]() は、観測値を理論式と誤差で表すので観測方程式と呼ばれます。
は、観測値を理論式と誤差で表すので観測方程式と呼ばれます。
このとき付録A2より
と変形され基本モデルと同じ形になります。
最小二乗の条件は、
が最小なることと言い換えられます。ここで
は、重み行列と呼ばれます。従って、最小二乗の条件は単なる二乗和=長さの二乗ではなく、重みが付いた長さの二乗=重み付き残差二乗和:![]() が最小になることです。
が最小になることです。
となり、最小二乗解は、
と求まります。この解は普通の最小二乗解と同じくBLUEとなります。
![]()
となります。
重みと分散
ある観測![]() の重み
の重み![]() は分散
は分散![]() に逆比例する量として定義されます。
に逆比例する量として定義されます。
分散が小さければその観測の重みは大きくなります。特に、各観測値![]() がおのおの独立で異なる分散
がおのおの独立で異なる分散![]() を持つとすると
を持つとすると
より、重み行列は
となります。![]() としたものが(2)で、基準となる観測
としたものが(2)で、基準となる観測![]() を選び
を選び![]() とすると
とすると![]() となりますから
となりますから![]() は単位重量当たりの分散あるいは基準分散と呼ばれます。時には各観測値の分散が既知の場合があります。その場合は、
は単位重量当たりの分散あるいは基準分散と呼ばれます。時には各観測値の分散が既知の場合があります。その場合は、![]() として、
として、![]() とすればよいのですが、
とすればよいのですが、![]() の値は最小二乗解には影響を与えません。
の値は最小二乗解には影響を与えません。
3.いくつかの例
ここで測量に関連した例を挙げてみたいと思います。
例1.水準測量
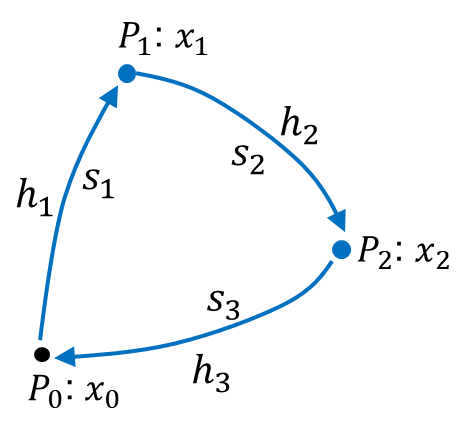
簡単な水準路線で未知点の標高を求めてみましょう(図1)。既知点![]() の標高が
の標高が![]() 、未知点
、未知点![]() 、
、![]() の標高が未知パラメータ
の標高が未知パラメータ![]() 、測定値は比高
、測定値は比高![]() です。
です。
の形に行列で書くと、
として、
となります。
水準測量の場合、観測の重みは路線長に反比例するという経験則があるのでそれを採用すると、重量行列は各路線長を![]() として
として
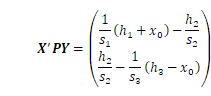
から(![]() の逆行列の計算は付録A2参照)、最小二乗解が
の逆行列の計算は付録A2参照)、最小二乗解が
と求まります。
この例は簡単な水準網でしたが、どのような水準網も観測値(比高)は未知パラメータである水準点標高の和や差で表せるので線形モデルになっています。
例2.基準点測量(距離測量による平面位置決定)
基準点測量は、距離、角度、GNSSなどの観測を使って新しい点の位置を求める測量です。点の座標と観測値は一般に非線形の関係ですから、テイラー展開(付録C参照)で線形化して(2)の形にすることで最小二乗法を適用します。
簡単な距離測量による平面位置の決定の問題(図2)について見てみましょう。
図2.距離観測による位置決定
![]() が既知点、
が既知点、![]() が未知点で
が未知点で![]() から
から![]() までの距離
までの距離![]() を測定したとします。観測の重みはそれぞれ
を測定したとします。観測の重みはそれぞれ![]() とします。
とします。
距離は位置座標によって次のように非線形関数で表されます。
未知座標を概算値(添字0)+補正量: ![]() としてテイラー展開すると(微分の詳細は略)、
としてテイラー展開すると(微分の詳細は略)、
となるので、各距離の観測方程式は、
となります。最小二乗解は例1と同様に計算できPの位置ベクトルが
![]()
と求まりますが、注意点が一つあります。観測方程式はあくまで非線形関数を近似した式のため、最初に解いた解には省略した項の影響が残っている可能性があります。従って、最初の解を概略値としてもう一度最小二乗解を求め、さらにこれを何回か繰り返し収束したものを最終的な解としています。測地網の場合、数学モデルが堅固なので普通、1回の反復改良計算で収束します。ただし、初期値と推定値が大きい場合、2回程度の反復改良計算が必要なことがあります。
例3.GNSS測量(二重位相差による相対測位)
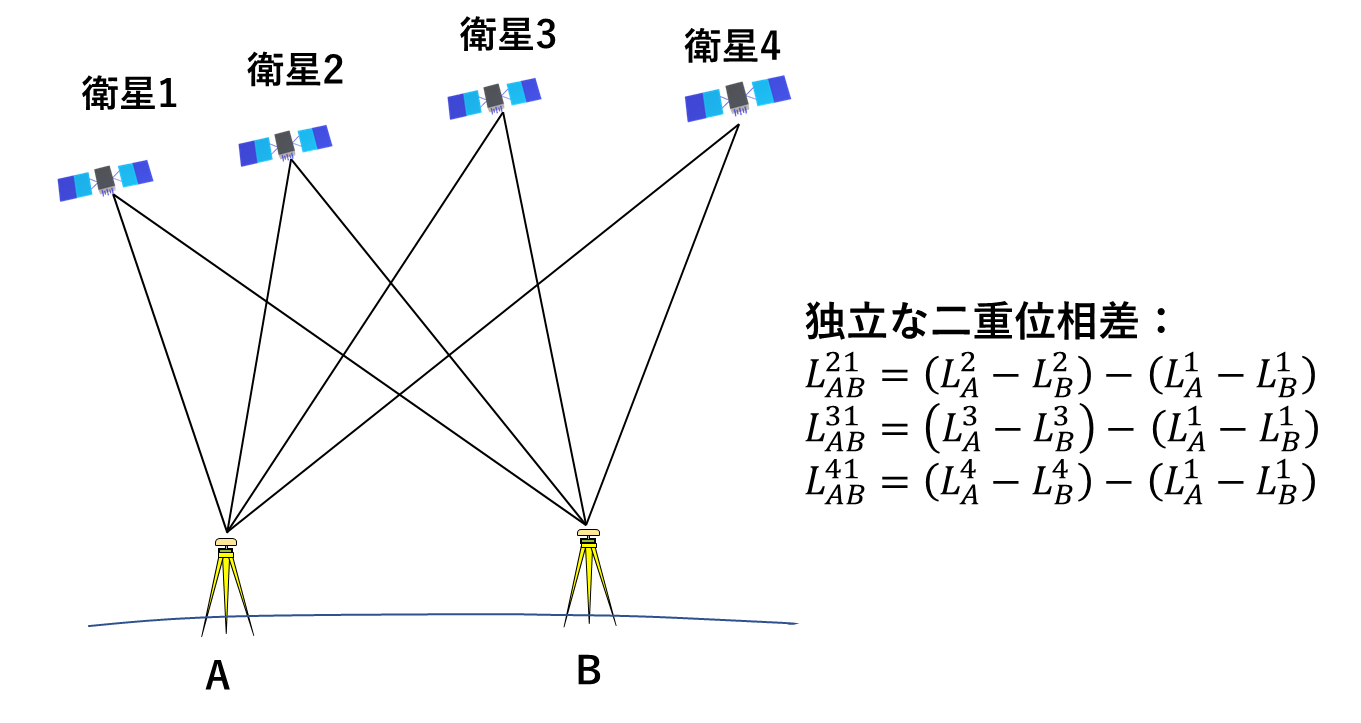
受信機を点A(既知点) とB(未知点)におき、Bの位置を位相観測による相対測位で決定する測量を考えましょう。精密測量では一般に二重位相差をとって時計誤差を消去します(図3)。
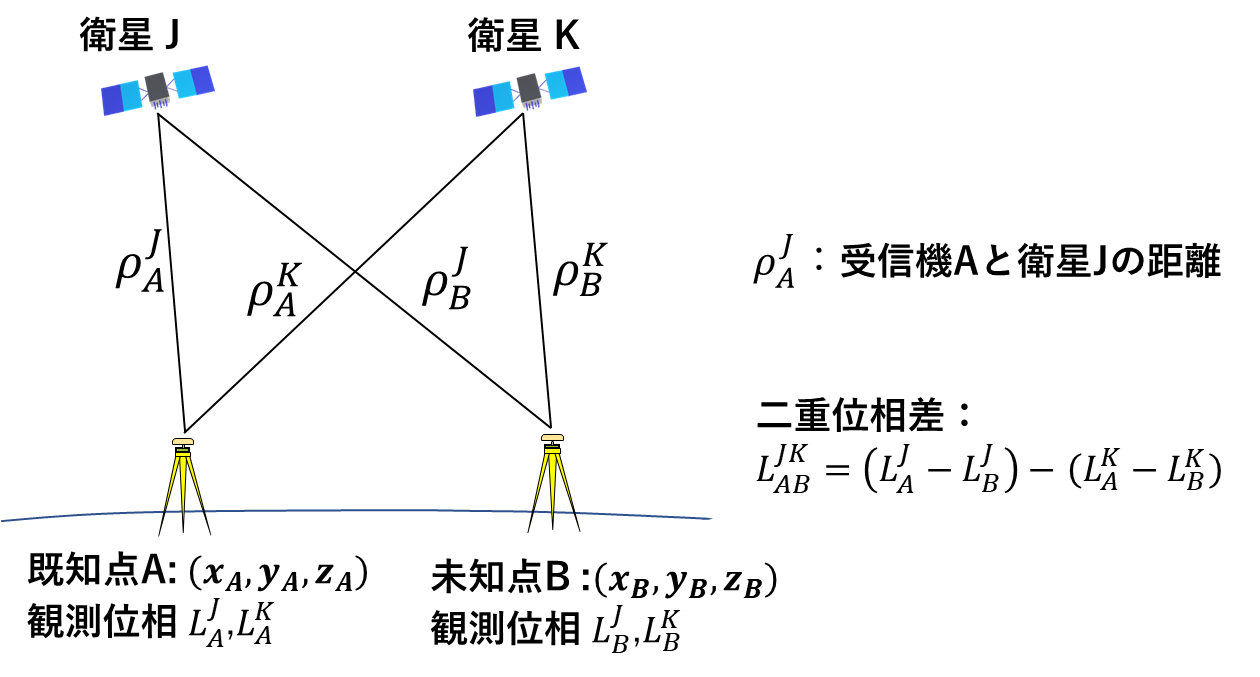 図3.二重位相差の観測
図3.二重位相差の観測
ここではABを短基線とし、大気による誤差も無視できるとすると単純化された観測方程式は次のようになります。
です。実際は、このような観測が衛星のペア×エポック数だけあります。 ![]() は受信機と衛星間の距離で位置座標の線形関数ではありませんから、例2と同様に線形化します。例えば、4衛星1エポックの観測からは3つの独立な二重位相差が得られ(図4)、未知数はBの座標(の補正量)と3つのアンビギュイティーの6つです:
は受信機と衛星間の距離で位置座標の線形関数ではありませんから、例2と同様に線形化します。例えば、4衛星1エポックの観測からは3つの独立な二重位相差が得られ(図4)、未知数はBの座標(の補正量)と3つのアンビギュイティーの6つです:![]() 。
。
図4.4衛星1エポックの二重位相差
![]() を線形化すると、計画行列
を線形化すると、計画行列![]() の
の![]() 番目のエポックに対応する行は、次のようになります。
番目のエポックに対応する行は、次のようになります。
微分を行うと、
などから、例えば
となります。行の数は観測の数と同じです。このようにして線形化された式を最小二乗法で解くわけですが、例1,2の場合と違うことがあります。それは、観測データ(二重位相差)の間に相関があることです。図4の二重位相差の式を見ると、一重位相差![]() が3つに共通に含まれていることからもわかります。各点での位相観測は独立と考えられ共分散行列は対角行列ですが、二重位相差は位相の線型結合になっています。二重位相差の観測値ベクトル
が3つに共通に含まれていることからもわかります。各点での位相観測は独立と考えられ共分散行列は対角行列ですが、二重位相差は位相の線型結合になっています。二重位相差の観測値ベクトル![]() は、位相観測値ベクトル
は、位相観測値ベクトル![]() を行列
を行列![]() で変換して,
で変換して,
と得られる(![]() の要素は+1、1、0のいずれかです)ので、
の要素は+1、1、0のいずれかです)ので、![]() の共分散行列は誤差伝播(前回参照)より、
の共分散行列は誤差伝播(前回参照)より、
と書け、この重量行列を用いて最小二乗解を求めることになります。