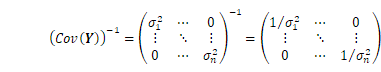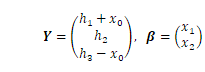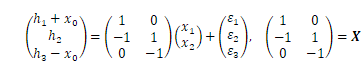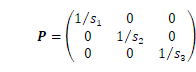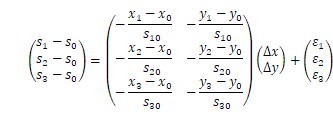誤差論と最小二乗法
第8回 線形モデル – その2
2020年03月17日
前回は基本の線形モデルを取り上げ、最小二乗法により未知パラメータを推定しました。今回は、もう一つの推定法である最尤法で未知パラメータを求めてみます。次に線形モデルを少し一般化したものを考えます。具体的には、![]() の場合です。各観測値の分散が異なる場合や相関を持つ場合に相当します。
の場合です。各観測値の分散が異なる場合や相関を持つ場合に相当します。
1. 最尤(推定)法
最小二乗法は線形モデルにおける基本的な方法ですが、様々なデータの中には線形モデルで記述するには不適切なものもあります。そのような場合に一般に用いられる方法が最尤法です。
最尤法は第6回に紹介しました。尤度関数を最大にする推定値を求める方法です。尤度関数とは観測値の確率密度関数において観測値は観測された値に固定し、パラメータを変数とみなしたものです。ここでは最尤法を正規分布の線形モデルに用いてみましょう。
線形モデル
![]()
において、観測値の分布を(n次元の)正規分布(付録B参照)
![]() の最尤推定値は上式の第3項を最大にするものですから残差二乗和
の最尤推定値は上式の第3項を最大にするものですから残差二乗和![]() を最小にするもの、つまり最小二乗法と同じになります。
を最小にするもの、つまり最小二乗法と同じになります。
最尤法は様々な分布を持つデータに用いることができる一般的な方法ですが、定義からもわかるように観測値の分布関数を仮定する必要があります。最小二乗法では特に分布関数の形に仮定はなく、分散(あるいは重み)のみが仮定されます。
2. 一般の最小二乗法
線形モデルにおいて各観測値の分散が必ずしも同じでない場合を考えます。すると、![]() を測定データ、
を測定データ、![]() を既知の計画行列、
を既知の計画行列、![]() を未知パラメータ、
を未知パラメータ、![]() をランダム誤差とするとモデルは
をランダム誤差とするとモデルは
と書けます。ここで、![]() は既知の正定値行列、
は既知の正定値行列、![]() は一般には未知とします。式
は一般には未知とします。式![]() は、観測値を理論式と誤差で表すので観測方程式と呼ばれます。
は、観測値を理論式と誤差で表すので観測方程式と呼ばれます。
このとき付録A2より
と変形され基本モデルと同じ形になります。
最小二乗の条件は、
が最小なることと言い換えられます。ここで
は、重み行列と呼ばれます。従って、最小二乗の条件は単なる二乗和=長さの二乗ではなく、重みが付いた長さの二乗=重み付き残差二乗和:![]() が最小になることです。
が最小になることです。
となり、最小二乗解は、
と求まります。この解は普通の最小二乗解と同じくBLUEとなります。
![]()
となります。
重みと分散
ある観測![]() の重み
の重み![]() は分散
は分散![]() に逆比例する量として定義されます。
に逆比例する量として定義されます。
分散が小さければその観測の重みは大きくなります。特に、各観測値![]() がおのおの独立で異なる分散
がおのおの独立で異なる分散![]() を持つとすると
を持つとすると
より、重み行列は
となります。![]() としたものが(2)で、基準となる観測
としたものが(2)で、基準となる観測![]() を選び
を選び![]() とすると
とすると![]() となりますから
となりますから![]() は単位重量当たりの分散あるいは基準分散と呼ばれます。時には各観測値の分散が既知の場合があります。その場合は、
は単位重量当たりの分散あるいは基準分散と呼ばれます。時には各観測値の分散が既知の場合があります。その場合は、![]() として、
として、![]() とすればよいのですが、
とすればよいのですが、![]() の値は最小二乗解には影響を与えません。
の値は最小二乗解には影響を与えません。
3.いくつかの例
ここで測量に関連した例を挙げてみたいと思います。
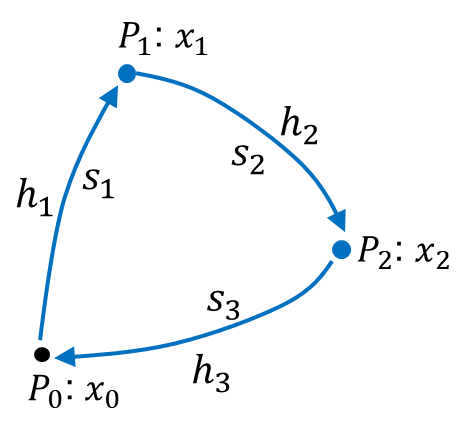
例1.水準測量
簡単な水準路線で未知点の標高を求めてみましょう(図1)。既知点![]() の標高が
の標高が![]() 、未知点
、未知点![]() 、
、![]() の標高が未知パラメータ
の標高が未知パラメータ![]() 、測定値は比高
、測定値は比高![]() です。
です。
の形に行列で書くと、
として、
となります。
水準測量の場合、観測の重みは路線長に反比例するという経験則があるのでそれを採用すると、重量行列は各路線長を![]() として
として
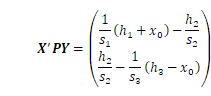
から(![]() の逆行列の計算は付録A2参照)、最小二乗解が
の逆行列の計算は付録A2参照)、最小二乗解が
と求まります。
この例は簡単な水準網でしたが、どのような水準網も観測値(比高)は未知パラメータである水準点標高の和や差で表せるので線形モデルになっています。
例2.基準点測量(距離測量による平面位置決定)
基準点測量は、距離、角度、GNSSなどの観測を使って新しい点の位置を求める測量です。点の座標と観測値は一般に非線形の関係ですから、テイラー展開(付録C参照)で線形化して(2)の形にすることで最小二乗法を適用します。
簡単な距離測量による平面位置の決定の問題(図2)について見てみましょう。
図2.距離観測による位置決定
![]() が既知点、
が既知点、![]() が未知点で
が未知点で![]() から
から![]() までの距離
までの距離![]() を測定したとします。観測の重みはそれぞれ
を測定したとします。観測の重みはそれぞれ![]() とします。
とします。
距離は位置座標によって次のように非線形関数で表されます。
未知座標を概算値(添字0)+補正量: ![]() としてテイラー展開すると(微分の詳細は略)、
としてテイラー展開すると(微分の詳細は略)、
となるので、各距離の観測方程式は、
となります。最小二乗解は例1と同様に計算できPの位置ベクトルが
![]()
と求まりますが、注意点が一つあります。観測方程式はあくまで非線形関数を近似した式のため、最初に解いた解には省略した項の影響が残っている可能性があります。従って、最初の解を概略値としてもう一度最小二乗解を求め、さらにこれを何回か繰り返し収束したものを最終的な解としています。測地網の場合、数学モデルが堅固なので普通、1回の反復改良計算で収束します。ただし、初期値と推定値が大きい場合、2回程度の反復改良計算が必要なことがあります。
例3.GNSS測量(二重位相差による相対測位)
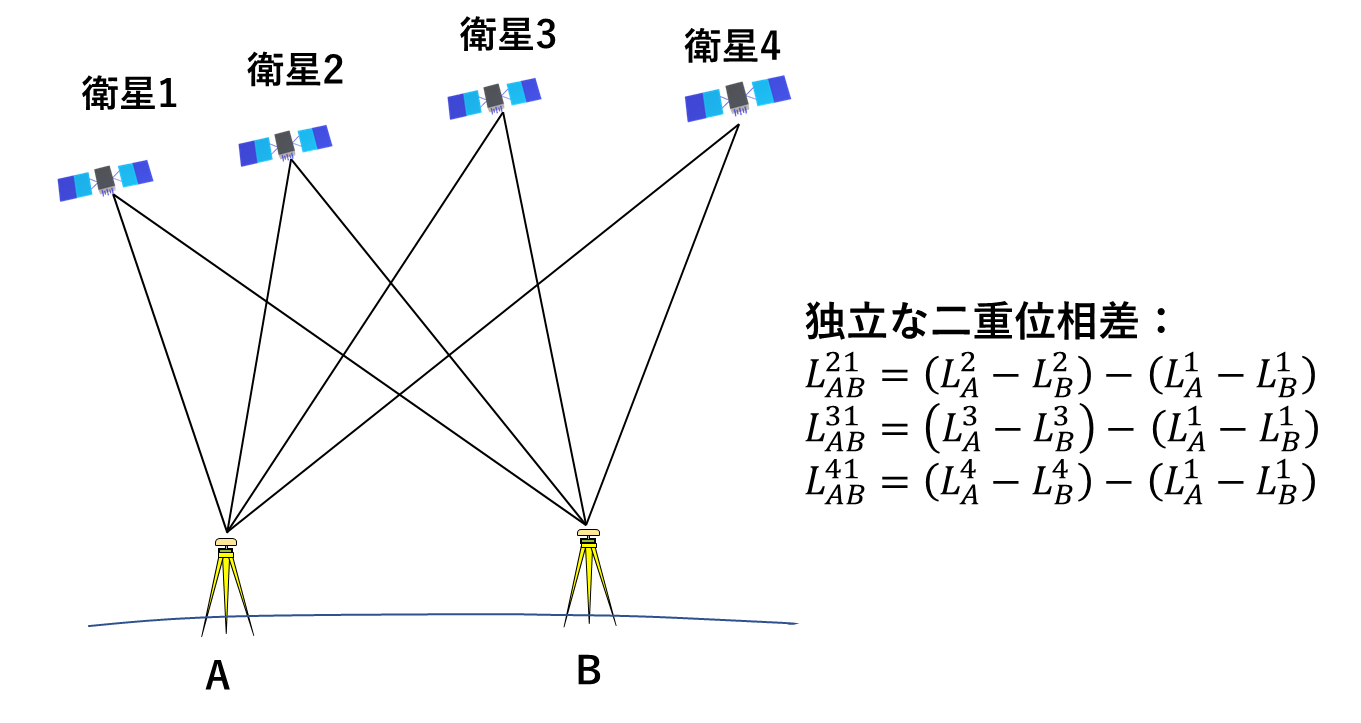
受信機を点A(既知点) とB(未知点)におき、Bの位置を位相観測による相対測位で決定する測量を考えましょう。精密測量では一般に二重位相差をとって時計誤差を消去します(図3)。
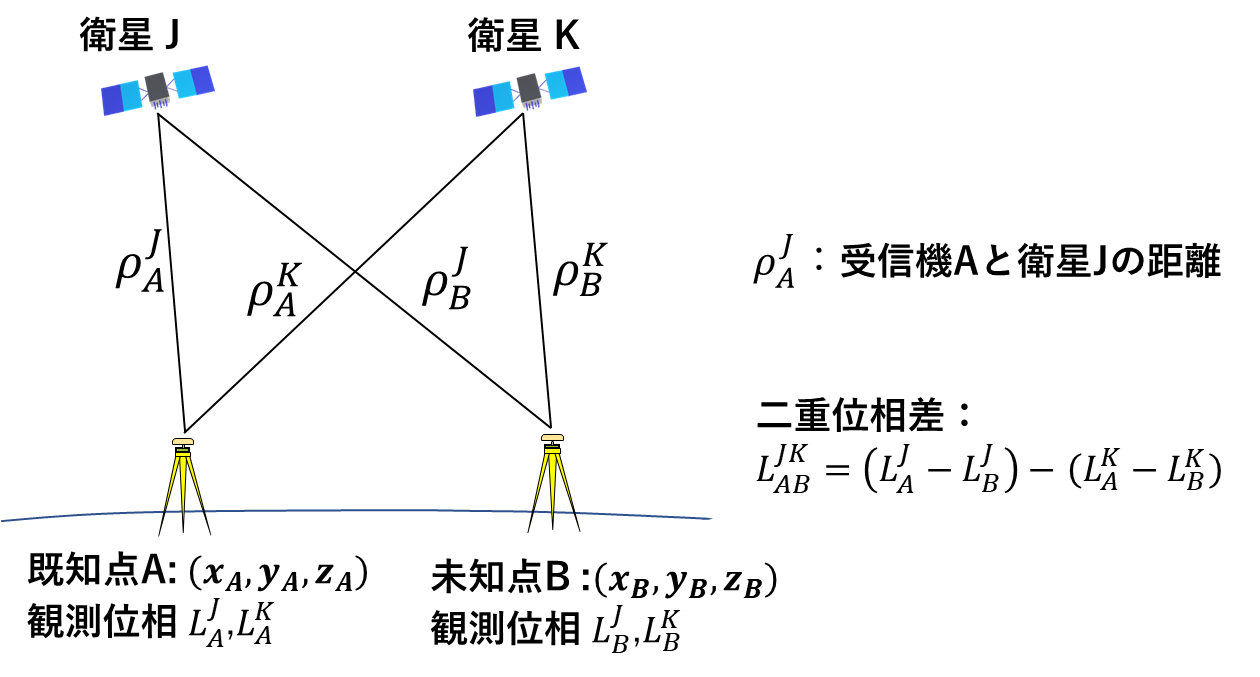 図3.二重位相差の観測
図3.二重位相差の観測
ここではABを短基線とし、大気による誤差も無視できるとすると単純化された観測方程式は次のようになります。
です。実際は、このような観測が衛星のペア×エポック数だけあります。 ![]() は受信機と衛星間の距離で位置座標の線形関数ではありませんから、例2と同様に線形化します。例えば、4衛星1エポックの観測からは3つの独立な二重位相差が得られ(図4)、未知数はBの座標(の補正量)と3つのアンビギュイティーの6つです:
は受信機と衛星間の距離で位置座標の線形関数ではありませんから、例2と同様に線形化します。例えば、4衛星1エポックの観測からは3つの独立な二重位相差が得られ(図4)、未知数はBの座標(の補正量)と3つのアンビギュイティーの6つです:![]() 。
。
図4.4衛星1エポックの二重位相差
![]() を線形化すると、計画行列
を線形化すると、計画行列![]() の
の![]() 番目のエポックに対応する行は、次のようになります。
番目のエポックに対応する行は、次のようになります。
微分を行うと、
などから、例えば
となります。行の数は観測の数と同じです。このようにして線形化された式を最小二乗法で解くわけですが、例1,2の場合と違うことがあります。それは、観測データ(二重位相差)の間に相関があることです。図4の二重位相差の式を見ると、一重位相差![]() が3つに共通に含まれていることからもわかります。各点での位相観測は独立と考えられ共分散行列は対角行列ですが、二重位相差は位相の線型結合になっています。二重位相差の観測値ベクトル
が3つに共通に含まれていることからもわかります。各点での位相観測は独立と考えられ共分散行列は対角行列ですが、二重位相差は位相の線型結合になっています。二重位相差の観測値ベクトル![]() は、位相観測値ベクトル
は、位相観測値ベクトル![]() を行列
を行列![]() で変換して,
で変換して,
と得られる(![]() の要素は+1、1、0のいずれかです)ので、
の要素は+1、1、0のいずれかです)ので、![]() の共分散行列は誤差伝播(前回参照)より、
の共分散行列は誤差伝播(前回参照)より、
と書け、この重量行列を用いて最小二乗解を求めることになります。